[原]boosted Tree学习笔记
陈天奇的几份材料很适合用来学习boosted Tree,
我强烈推荐各位看看。 【详细链接在文末】
本文是我的个人学习笔记,水平有限,敬请指教。
boosted Tree算法简要描述:
不断地添加树,不断地进行特征分裂来生长一棵树。
每次添加一个树,其实是学习一个新函数,去拟合上次预测的残差。
一个树是这样生长的,挑选一个最佳特征的最佳分裂点,来进行特征分裂。
训练后会得到的模型是多棵树,每棵树有若干叶子节点,每个叶子节点对一个分数,
假如来了一个样本,根据这个样本的特征,在每棵树上会落到对应一个叶子节点,
总分数就是把落到的叶子节点的分数加起来,作为预测值。
带着以下问题来理解这个算法:
1 如何生长一棵树?每次特征分裂怎么寻找最佳特征,怎么寻找最佳分裂点?
2一棵树什么时候停止生长?
3 假如一棵树的结构确定了,每个叶子节点的分数怎么求?
注意,下面讲解的时候,对于上面问题,理解的顺序是3,1,2。
模型和目标函数
我们的模型是要学习K棵树,每次去拟合上一次学习的残差。
跟传统有监督算法一样,目标函数由损失函数和正则项组成。
与传统决策树不同的是,传统的决策树中每次决策是Heuristic(启发式)的(比如信息增益),而这里,每次决策都是Objective(目标性质的,与目标函数相关)。
注意,陈天奇讲解推导boosted tree与传统gbdt的一个不同点,前者将损失函数抽象出来了,不用具体的损失函数。这种抽象,更加简明扼要。而且这个算法工程化的版本xgboost正也有个优点就是,可以任意自定义损失函数。
如何理解每一棵树,拟合的是上一次学习的残差呢?
下面是一个直观感受
可以看到,每一轮新的预测,是上次预测值+本次学习的函数。
把最新的一次预测拆分成 上次预测值+本次学习的函数
目标函数中,目标值和上次预测值都是已知的,
那么唯一要求的是新的函数,【先忽略后面的正则项】
使目标函数最小。
根据泰勒二级展开对目标函数进行变形
可以看到,现在的目标函数的已知部分是
1 上次预测的损失函数对应函数值
2 上次预测的损失函数的一级偏导数对应函数值
3上次预测的损失函数的二级偏导数对应函数值
这一些值根据上次预测结果可以求出来,唯一未知的就是新函数。
而我们这里,是用一个棵树表示一个函数,每个叶子节点的输出值就是函数值,可枚举的。
我们的目标就是把这些叶子节点的输出值求出来,使得目标最优。
树的定义
q代表树结构,输入一个样本的特征给q,会落到唯一对应的叶子节点,返回该叶子节点的编号。w代表叶子权重,输入一个叶子节点编号给w,返回对应的权重。
f就是整棵树的定义,正是我们所求,
输入一个样本特征,落到唯一的节点,把节点对应的权重返回作为分数输出。
再次强调,我们的目标就是,把每个节点对应的权重求出来,使得目标函数最小化。
树的复杂度定义
这个就是正则项,由叶子节点数量以及对应权重的平方和组成。
目标函数变形:
之前损失函数的描述,是一个个样本(从1到n)的损失值求和。
这里,以每个叶子节点对应的样本作为一组,
这样就可以将叶子节点对应的权重作为公因式提取出来。
可以看到,T个叶子节点的权重是未知项,其他都是已知的。
每个叶子节点的权重求解
对于每个叶子节点的权重,都是一个一元二次函数。
一元二次函数的最小值就是那条抛物线的最低点,高中知识。
对于这里,为什么可以对每个叶子节点分别求最小值呢?
我的理解是,因为每个叶子的权重互相独立,互不影响。
当每个叶子节点对应的目标函数值最小,那么总的目标函数值就最小。
到目前为止,我们已经知道,
假如已知一棵树,那么根据上次预测的损失函数一阶导数和二阶导数对应函数值,
就可以把这棵树的叶子节点权重和目标函数最小值求出来。
那么,穷举所有树的可能性,最优解就是目标函数值最小的结果对应的树。
但是实际上,我们并不会这么干。
我们采取贪心算法来生长一棵树,
每次找一个最优的特征进行分裂,
每个特征是寻找最优点进行分裂,
知道到达一定的深度或者不能再分裂(分裂后损失值更大)。
最优特征?最优分裂点?如何衡量这个最优呢?
假如我们选定一个特征,任意一个点作为分裂,
如何量化这次分裂的效果呢?
还是以目标函数值为标准,对比分裂前和分裂后的最小目标函数值。
所以,选定了一个特征,从左往右根据一定的步长扫描,
求出每个分裂点的增益,找到增益最大的点作为分裂点即可。
那么,每一次选特征时,
就是遍历所有特征,求出每个特征对应的最佳分裂点。
把增益最大的特征和分裂点作为下一次特征分裂。
于是,生长一棵树的算法如下:
对于每个节点,枚举所有特征进行以下操作:
对于每个特征,根据特征值对样本进行排序
从左到右扫描,根据分裂增益寻找最佳分裂点
从所有特征中,选取分裂增益最大的特征分裂。
值得注意的是,什么时候停止生长?如何剪枝?
boosted算法概述:
整个算法的理解如下,
a 每次迭代添加一棵树
b 每次迭代前,求出上次预测损失函数一阶导数和二阶导数的函数值
c 根据分裂增益最大化,去生长这棵树
d 把新的树添加到原来模型(新的树可以乘上一个系数,防止过拟合)
至此,整个算法的核心理念讲解完毕。
当然,至于算法如何分布式高效实现,本文尚未涉及,后续有空看看xgboost的论文再续分享。
XGBoost 与 Boosted Tree
Introduction to Boosted Trees, Tianqi Chen 【slides】
http://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
XGBoost: A Scalable Tree Boosting System 【slides】
http://papail.io/teaching/901/day3/ScottZhenyu.pdf
XGBoost: A Scalable Tree Boosting System 【paper】
http://www.kdd.org/kdd2016/papers/files/rfp0697-chenAemb.pdf
本文作者:linger
本文链接:http://blog.csdn.net/lingerlanlan/article/details/69641734
转载须注明出处
欢迎关注公众号:数据挖掘菜鸟【公众号ID:data_bird】
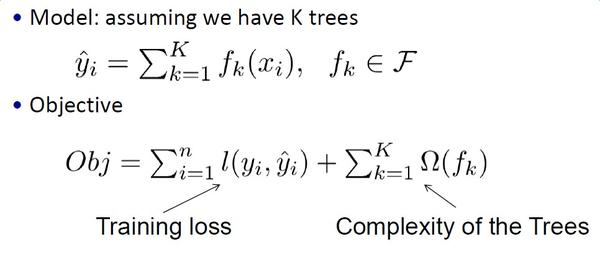

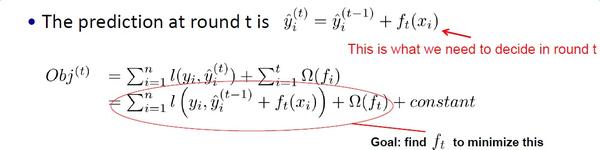
 可以看到,现在的目标函数的已知部分是
可以看到,现在的目标函数的已知部分是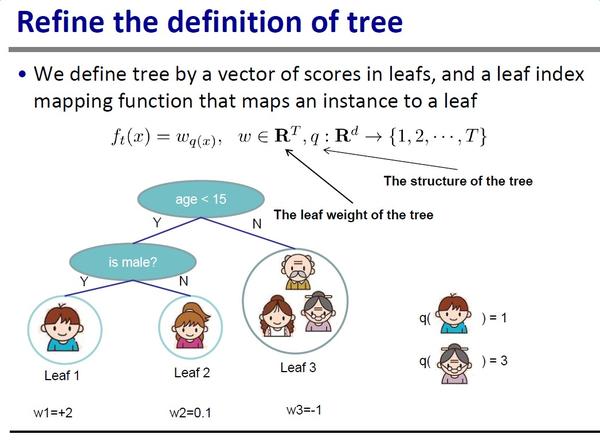
 这个就是正则项,由叶子节点数量以及对应权重的平方和组成。
这个就是正则项,由叶子节点数量以及对应权重的平方和组成。

 所以,选定了一个特征,从左往右根据一定的步长扫描,
所以,选定了一个特征,从左往右根据一定的步长扫描,


