PRML读书会第十三章 Sequential Data

主讲人 张巍

（新浪微博: @张巍_ISCAS）

软件所-张巍 19:01:27
我们开始吧，十三章是关于序列数据，现实中很多数据是有前后关系的，例如语音或者DNA序列，例子就不多举了，对于这类数据我们很自然会想到用马尔科夫链来建模：

例如直接假设观测数据之间服从一阶马尔科夫链，这个假设显然太简单了，因为很多数据时明显有高阶相关性的，一个解决方法是用高阶马尔科夫链建模：

但这样并不能完全解决问题 ：1、高阶马尔科夫模型参数太多；2、数据间的相关性仍然受阶数限制。一个好的解决方法，是引入一层隐变量，建立如下的模型：

这里我们假设隐变量之间服从一阶马尔科夫链，观测变量由其对应的隐变量生成。从上图可以看出，隐变量是一阶的，但是观测变量之间是全相关的，今天我们主要讨论的就是上图中的模型。如果隐变量是离散的，我们称之为Hidden Markov Models；如果是连续的，我们称之为: Linear Dynamical Systems。现在我们先来看一下HMM ，从图中可以看出，要完成建模，我们需要指定一下几个分布：
1、转移概率：

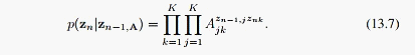
2、马尔科夫链的初始概率：

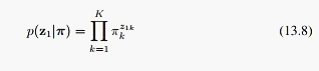
3、生成观测变量的概率(emission probabilities)：

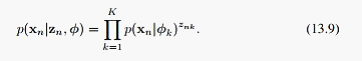
对于HMM， 这里1和2我们已经假设成了离散分布，由隐变量Zn生成观测数据可以用混合高斯模型或者神经网络，书上的Zn是一个k维的布尔变量，由此再看隐变量转移概率公式、观测数据的生成公式就容易理解了。模型建好了，我们接下来主要讨论下面三个问题：
1、学习问题：就是学习模型中的参数；
2、预测问题：即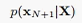,给定当前序列预测下一个观测变量；
3、解码问题：即p(Z|X)，给定观测变量求隐变量，例如语音识别；

游侠(419504839) 19:24:21
什么是解码问题？
软件所-张巍 19:25:18
例如观测到了一段语音，要求识别其对应的句子。@游侠 我前面没怎么举例子，不知道这样说清楚没？
游侠(419504839) 19:27:20
这个和一般说的”推断”一样不
软件所-张巍 19:28:27
这个也可以叫推断，只是推断是个比较一般的词汇。
我们来看一下HMM有多少参数要学，对应于刚才说到的三个分布，我们也有三组参数要学。
球猫(250992259) 19:30:46
其实就是假设东西是一个马尔科夫模型生成的。。然后把参数用某种方法弄出来，最后根据模型的输出来给答案……是这样吧？

软件所-张巍 19:32:45
@球猫 对，都是这个思路，先把参数学出来，然后就可以做任何想要的推断了，在这里所谓的解码问题只是大家比较关心。
软件所-张巍 19:32:51
好，继续，我们先来看1、学习问题。这里我们用EM算法来学习HMM的参数：
1、是转移概率对应的转移矩阵；
2、初始概率对应的离散分布参数；
3、观测变量对应的分布参数（这里暂不指定）。
用EM我们要做的就是：
E步里根据当前参数估计隐变量的后验：

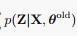
M步里最大化下面的期望：

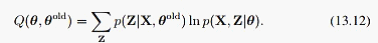
先来看M步，这里相对简单一点，整个模型的全概率展开为：

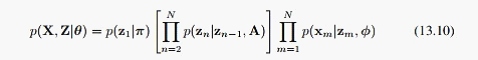
把13.10代入13.12,我们会发现计算时需要下面两个式子：
和
为了方便，我们就定义：

这样我们在E步就主要求出这两个式子就行了，当然这也就意味着求出了整个后验，利用这两个式子，13.12可以化为：

这个时候就可以用一些通用方法，例如Lagrange来求解了，结果也很简单：

对于观测变量的分布参数，与其具体分布形式相关，如果是高斯：，对应的最优解为：

如果是离散：对应的最优解为：

好，M步就这样， 现在来看E步，也是HMM比较核心的地方。刚才我们看到，E步需要求的是：
由马尔科夫的性质，我们可以推出：

其中：

接下来我们就建立和的递推公式

其中：

这样我们从开始，可以递推出所有的，对于，也进行类似的推导：

从上式可以看到是一个逆推过程，所以我们需要初始值，定义13.35并没有明确的定义：

因为z_N后没有观测数据，不过我们可以从，得出:

这样就等于1，现在我们可以方便的求出所有的和了，利用13.13也就可以求出所有的。类似的，我们可以求出：

这样在M步里求解所需要的分布就都求出来了，也就可以用EM来学习HMM的参数了，这里式子比较多，大家自己推一下会比较好理解。

第一个学习问题就这样了，接下来是预测问题，预测问题可以直接推导：

现在就剩最后一个解码问题，也就是argmax_Z{p(Z|X)}，刚才我们在E步已经求出了：

但是现在的问题要复杂一点，因为我们要求概率最大的隐变量序列，用13.13可以求出单个隐变量，但是他们连在一起形成的整个序列可能概率很小，这个问题可以归结为一个动态规划：

我们把HMM化成如上图的样子，最大化后验等价于最大化全概率，对于上图中的边，我们赋值为：
log（）
初始节点赋值为：
log(*p(x_1|z_1)）
其余节点赋值为：
log()
这样任何一个序列Z，其全概率等于exp（Z对应路径上节点和边的值求和），这样，解码问题就转化为一个最长路径问题，用动态规划可以直接求解。大家看这里有没有问题，HMM的主要内容就是这些

接下来的Linear Dynamical Systems 其实和HMM大同小异，只是把离散分布换成了高斯，然后就是第二章公式的反复应用，都是细节问题，就不在这里讲了，大家看看有问题我们可以讨论。这一章还是式子主导的，略过了不少式子，大家推的时候有问题我们可以随时讨论。

天涯游(872352128) 21:09:21
我对hmm 的理解，觉得这麻烦的是概率的理解的了，概率分解才是hmm的核心，当然了还有动态规划了。概率分解其实是实验事件的分解，如前向 和后向了，还有就是EM算法了。

注：PRML读书会系列文章由 @Nietzsche_复杂网络机器学习 同学授权发布，转载请注明原作者和相关的主讲人，谢谢。

PRML读书会讲稿PDF版本以及更多资源下载地址：http://vdisk.weibo.com/u/1841149974

本文链接地址：http://www.52nlp.cn/prml读书会第十三章sequential-data