SGU 150 - 159 解题报告
151 Construct a triangle 解析几何
152 Making round 贪心
153 Playing With Matches 博弈 + 规律
154 Factorial 初等数论
155 Cartesian Tree RMQ
156 Strange Graph 欧拉回路
157 Patience 模拟打表
150 Mr. Beetle II
枚举
题意:给定两个二维坐标上的点(x1, y1)、(x2, y2),坐标范围为[-106, 106]。求从一个点(x1, y1)到(x2, y2)的直线路径上经过的第N个方格的左下角坐标,无解输出no solution。
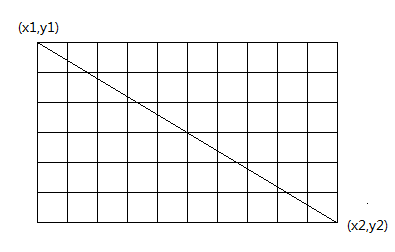
图1
题解:首先,如果两个点的x坐标相同或者y坐标相同,则直接无解;否则将(x1, y1)和(x2, y2)一起做相应的平移,使得(x1, y1)和(0, 0)重合,方便计算。
如果x1 < x2,枚举x坐标属于(x1, x2],对于每个单位为1的区间[x, x+1]容易计算出y方向上有多少个方格,统计出第n个方格;如果x1 > x2,枚举x坐标属于(x2, x1],用同样的方法进行计算。
151 Construct a triangle
解析几何
题意:给定三角形的两条边AB = c、 AC = b 和 一条中线 AM = m 的长度,求一个满足条件的三角形的坐标。
题解:由于三角形的坐标可以随意取,所以为了简化问题,可以将A点定在坐标原点,B点定在x轴正方向,C则在第一象限或者第二象限;
假设A在原点(0, 0)
B在x+轴上,则有B点坐标(c, 0)
假设C点坐标为(x, y), 中线坐标为 (B + C) / 2,即 ( (x+c)/2, y/2 )
已知AM距离m 和AC距离b,则有:
x2 + y2 = b2 (1)
((x+c)/2)2 + (y/2)2 = m2 (2)
合并(1) (2),则有
-2cx - c2 = b2 - 4 * m2 (3)
x = (4*m2 -b2 - c2)/2/c; (4)
y2 = b2 - x2; (5)
根据(5),可以推出 y2 = b2 - x2 = b2 - ((4*m2 -b2 - c2)/2/c ) 2 =>[ (b+c) 2 - (2m)2 ] * [ - (b-c)2 + (2m)2 ] > 0
b+c > 2m 并且 2m > fabs(b-c)时y才有解,所以当 2*m > (b+c) 或者2*m < fabs(b-c) 为无解的情况。
而我们假设C在第一象限或者第二象限,所以y>0,于是(x, y)可通过(4) (5)求得。
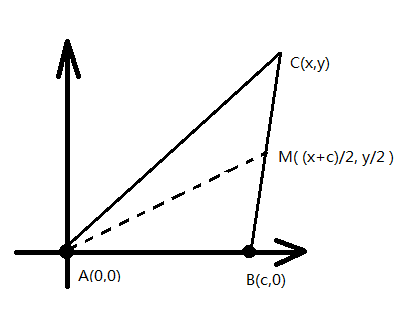
图2
152 Making round
贪心
题意:给定N(N <= 10000)个数,求每个数在所有数中所占百分比,要求输出的数之和为100,每个数可以进行上下取整。如:给定三个数3 3 3,那么输出为 34 33 33。34为向上取整的结果,33为向下取整的结果。
题解:
1)首先求得所有数之和S,将每个数a[i]除上S得到商B[i]和余数M[i]。
2)如果余数为0表示为整除,不能进行上下取整。如果余数不为0,说明它有 +1 或者 +0 的机会。 (因为题目说可以上取整,也可以下取整)
3) 记录下所有余数不为零的个数T。
4)将所有数的商之和Sum{B[i]} 和 余数不为零的数的个数T 相加,如果小于100,则表明必定无解。否则扫描数组,将 X = 100-Sum{B[i]}-T 的值分派给每个不能整除的数即可(每个数只可分派1)。
153 Playing with matches
博弈
题意:给定N根火柴(N <= 109),每次可以从这些火柴中取1,P1,P2,...,Pm (2<=Pi<=9, 0<=m<=8)根,两人分别轮次进行拾取,并且总是按照最优策略去取,最后取完火柴的人为输的人,问当前状态是否是一个必胜状态。
题解:经典博弈,对于给定状态X:
1) 如果按照所有方式取,最后都只能让对手到达必胜状态,那么X为必败状态;
2) 如果对于某种取法,可以让对手达到必败状态,那么X为必胜状态;
3) 显然,0为必胜态,1为必败态,2为必胜态。
根据以上的性质,可以通过递推,将火柴根数确定的情况下,将所有状态算出来,但是由于N <= 109,数据量太大,但是我们注意到每个Pi很小,最大值也只有9,某些大状态是通过小状态算出来的,所以必然存在循环。
于是问题就转化成了求一堆序列的循环节,可以先预处理将5000(足够大就行)以内的状态用记忆化搜索算出来,对于每个状态值,用0表示必胜,1表示必败。枚举循环节的长度len,然后检测是否一个合法的循环节。最后N的状态值就是N % len的状态值。
154 Factorial
二分统计 + 初等数论
题意:给定一个数N,求一个最小的数K,使得K!末尾正好有N个0。
题解:因为K!中的质因子中5的个数明显比2的个数少,所以求末尾有多少个0,其实就是求K!中有多少个质因子5。那么这些质因子一定出现在 5、10、15、25、30、35、... K中,对于 K!,将所有的5的倍数提出来,剩下部分为T,则有:
K! = 1*2*3*4*5*...(K-1)*K = 5 * 10 * 15 * ... * (1*2*3*4*6*7*8*9*11*12*13*14*16*...K) = 5*10*15*...* T = 5* (1*2*3...) * T = 5 * T * K'! , 我们发现5*T中5的质因子个数为T个,K'! 中的5的个数则可以转化成子问题求解,这样就变成了一个递归求解K中质因子为5的个数S的问题,递归方程为 S[ K ] = K/5 + S[K/5] ( K > 0 ) 当K = 0时返回0,即递归出口。
那么就可以二分枚举一个K,然后通过上面的递归求解K中5这个质因子的个数,然后和N比较,如果找不到一个K,使得它的5质因子的个数为N则无解,否则找一个最小的。
155 Cartesian Tree
RMQ(or ZigZag)
题意:给定N(N <= 50000)个整数对(key, a),要求将他们组织成一棵树二叉树,并且对于树的任意一个结点,满足如下两个性质:
1) 当前结点的a值大于它父节点的a值(小顶堆的性质);
2) 当前结点的key值大于左子树的key值,并且小于右子树的key值(排序二叉树的性质);
题目保证所有的key值和a值都不同。
题解:首先将所有整数对按key值递增排序,这样我们只需要对数组进行切分,如果第t个结点作为根结点,那么[1, t-1]必定是它的左子树集合,[t+1, N]必定是它的右子树集合,这样就能够保证第二个条件,而第一个条件需要满足父节点的a值小于左右子树的a值,所以第t个结点必定是所有数中a值最小的,于是可以规约出一个递归算法,对于当前区间[l, r],找到区间内a值最小的作为根结点,然后将它左边的区间和右边的区间进行相同的递归运算。初始区间为[1, N],当[l, r]满足 l > r即为递归出口。求区间最小值可以采用RMQ。总的时间复杂度为排序的时间复杂度O(N log N)。
RMQ 资料参阅 http://www.cppblog.com/menjitianya/archive/2014/06/26/207420.html
156 Strange Graph
欧拉回路
题意:给定一个N(N <= 10000)个点的连通图,这个图满足以下性质:
1) 每个顶点v的度数都大于等于2;
2) 如果顶点v的度数等于2,那么它连接的两个顶点不相邻;
3) 如果顶点v的度数大于2,那么和v相邻的点u满足以下条件之一;
a) u的度数等于2;
b) 任何和v相邻的点(除了u)中都两两相邻;
求这个图的一个哈密尔顿回路(经过每个顶点一次的回路)。
题解:首先将所有度数为2的点进行标记,那么从这个图的定义中可知,未标记的点必定是在一个完全子图中的,将图中所有完全子图中的点缩成一个点,对缩完点的图统计度数,如果所有的点的度数都为偶数,那么必定存在一个欧拉回路,求出欧拉回路后再拆点转换成哈密尔顿回路;否则,欧拉回路不存在,哈密尔顿回路也就不存在。
157 Patience
打表题
题意:给定N(1 <= N <= 13),表示(1 2 3 ... N 空)这N+1个位置,其中N个位置随机排放着1-N中的某一张牌,每次可以在“空”左边的位置找到一张牌K,然后将K+1这张牌放在“空”的位置上,问哪些初始状态可以到达一个状态使得前N个格子的牌有序排列(第N+1个位置留空)。
题解:从(1 2 3 ... N 空)这个状态起,反向模拟,能够到达的状态都是可达状态,统计所有可达状态的个数,N的最大值为13,时间上不允许可以客户端计算出值然后打表!
158 Commuter Train
二分枚举
题意:车站长度为L(L <= 5000),给定N(N<= 300)个乘客在车站的位置,以及一辆公交车的M(M <= 300)个车门离车头的位置,乘客一定会选择离自己最近的车门进入,问这辆车要停在哪里可以使得所有人进入车门需要走的距离总和最大,好变态的想法。
题解:只要枚举车需要停靠的位置,然后枚举每个人到达的那个车门花费的距离总和,取最大值就是答案。
这里对于某个人需要去哪个车门可以采用二分枚举,因为车门是有序的,只要二分找到离它最近的左车门,那么下一个就是最近的右车门(需要考虑边界,最左和最右的情况都只有一个车门),然后取左、右车门的距离小者。仔细想一下,最大值不一定出现在整点上,也有可能出现在0.5的位置上,所以可以将所有坐标都乘2,然后最后答案再除二避免精度误差。
159 Self-Replicating Numbers
深度优先搜索
题意:求N(N <= 2000)位B进制数中平方的最后几位等于该数本身的数的个数。
题解:利用dfs从最后面一位digit开始枚举[0, B),模拟相乘后对应位的余数,如果和该数的枚举那一位不相符则不进行下一步搜索,当枚举到第N位完毕,则将解保存,这里需要注意当N为1的时候,最高位可以为0,否则最高位为0的情况需要去掉(最高位为0说明它不是N位数(N>1))。