Southeastern Europe 2004 解题报告
PKU 1961 http://poj.org/problem?id=1961
题意:给定一个长度为N(N <= 106)的字符串S,求它的所有前缀中能够表示成AK的前缀,并且要求求出每个前缀对应的K。
题解:KMP
利用KMP求出该串的Next数组,然后枚举每个前缀,根据Next数组的定义,对于某个前缀S[1...i],有S[1...Next[i]] = S[i-Next[i]+1...i],假设前缀S[1...i]能够表示长AK的形式,则A = S[Next[i]+1...i],所以必须满足i能够被i - Next[i] 整除,满足条件后K = i/( i - Next[i])。
B. Corporative Network
PKU 1962 http://poj.org/problem?id=1962
题意:给定N(N <= 20000)个点和M(M <= 200000)次操作,每次操作有两种类型:
I a b 将a的父结点设为b,并且合并距离为 |a-b| mod 1000
E a 询问a到根结点的合并距离。
题解:并查集
利用路径压缩的思想,用dist[p]表示p和p的父结点的合并距离,每次查询的时候累加p到根结点的合并距离,并且将p到p所在树的根结点R的路径上的所有点的父结点都设为R,然后更新各自的合并距离。
合并操作O(1),查询操作总复杂度O(N)。
C. Cave Exploration
PKU 1963 http://poj.org/problem?id=1963
题意:给出N(N <= 1000)条水平或者垂直的走廊,再给定走廊上任意一个坐标点作为起点以及方向,按照以下策略走:能够左转就左转,不能则笔直走,不能笔直走就右转,都不能就掉头。这样走最后绕一圈又会回到起点,问哪些走廊是没有经过的,只要有一个点走过就算经过。
题解:模拟 + 哈希。
将水平线段和竖直线段分开存,分两种情况讨论:
1、水平线段
对于任意一根水平线段,枚举所有的竖直线段,计算出交点和水平线段的端点,保存下来并且按x坐标递增排序,去掉重复点,利用双向链表将两个相邻点连接起来,由于x和y坐标范围为-32767~32767,而交点数不会超过N2,所以可以采用哈希将二维的点映射到一位数组中。每个点记录水平走廊的编号。
2、竖直线段
同上操作,不同的是每个点记录竖直走廊的编号。
经过1和2两步操作后,走廊上的关键点已经被离散化了,并且所有点都通过四向链表串接起来,然后只需要从起点开始模拟行走即可,走到一个关键点,将关键点所在的两个走廊编号标记掉,最后统计没有标记的走廊编号就是答案了。
D. City Game
PKU 1964 http://poj.org/problem?id=1964
题意:给定一个M*N(M <= 1000,N <= 1000)的01矩阵,求它的一个子矩阵,满足矩阵元素全为1,并且面积最大。
题解:枚举行,对于第i行,以第i行为起点,扫描每一列j,找到第一个不是1的数所在的位置P[j],令K[j] = P[j] - i,于是问题转化成了一个一维的问题。
L[i] 表示 K [ L[i]+1 ... i] 中的元素都大于等于K[i],但是L[i]小于K[i];
R[i] 表示 K [i ... R[i]-1] 中的元素都大于等于K[i],但是R[i]小于K[i];
Max{ (R[i] - L[i] - 1) * K[i], 1 <= i <= N }就是以当前枚举行为起点的最大矩阵,枚举M次取最大值就是全局的最大子矩阵了。
E. Cube Root
PKU 1965 http://poj.org/problem?id=1965
题意:给定一个不超过150个数字的正整数,求它的三次方根,精确到小数点后10位。
题解:大数模拟
将输入的数X用字符串存储,乘上1030,利用二分求出最大的Y,使得Y3 <= X。然后在Y的后十位前插入一个小数点,输出即可。
F. Cable TV Network
PKU 1966 http://poj.org/problem?id=1966
题意:求图的点连通度。给定一个N(N <= 50)个点的图,求去掉至少多少个点能够将它变成一个非连通图。
题解:搜索 + 剪枝 (或者 最大流)
枚举每个点去掉或不去掉,总共250种状态,每次去掉点后判断当前图的连通性,一旦破坏了连通,去掉的点数即为答案;如果发现某个点去掉后,剩下点组成的图变成了一个完全图,那么不用继续搜索了,因为当前状态下不可能将剩下的图变成非连通图了;如果去掉的点数超过目前的最优解也直接剪枝。
好吧...一定是数据弱了-_-||,正解是最大流拆点。
G. Alibaba
PKU 1967 http://poj.org/problem?id=1967
题意:给定N(N <= 104)个整数对(Pi, Di)表示在Pi位置有一个宝物,并且需要在Di 时间之前取走(给出顺序为Pi递增的顺序)。起始可以任意选择一个位置,往左或者往右取宝物,问是否能够保证每个物品都在Di时间之前取走(时间和距离关系为1:1),如果可以,给出取完所有宝物的最少时间。
题解:搜索 + 剪枝
首先可以想到的是,起始位置一定是N个宝物所在位置中的其中一个,所以首先可以枚举每个宝物的起始点,比如当前位置为pos,那么在第0秒内,访问过的区间为[pos, pos],可以选择往左走,也可以选择往右走,那么是不是只要选择某个方向走完,然后再反方向走到底如果能够满足所有点都在截止时间内完成一定是对的呢?答案是否定的,来看一组数据,如图1,起始点只能选择3号位置,并且只能选择往右走,走到4后再折回走到2,然后再折回走到5,以此类推,并且只有这一种路径才能满足所有宝物都在截至时间内取完。
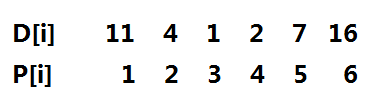
图1
按照这个思路,进行状态的划分,假设当前已经访问的区间为[L, R],并且现在的位置处于pos位置(这里pos要么等于L,要么等于R),所以可以用三维来表示状态DP[s][l][r](l、r表示访问过的区间的左右端点,如果当前位置在l则s = 0,如果当前位置在r,则s=1),总共状态数目N2,状态转移的时候由大状态推小状态,即DP[s][l][r]一定是由DP[0][l-1][r]、DP[0][l][r+1]、DP[1][l-1][r]、DP[1][l][r+1]这四个状态得出。
考虑到N比较大,所以把所有状态存储到数组中再利用动态规划进行递推,如果数据量不多的话,可以卡过,但是状态存储需要用滚动数组,否则内存吃不消,也可以采用搜索 + 剪枝,思路是沿用了动态规划的思想,假设当前已经访问的区间为[L, R],现在的位置处于pos位置(这里pos要么等于L,要么等于R),并且已经使用了T的时间,无论当前的pos是在左区间端点L上还是在右区间端点R上,他都可以选择走到L-1(L > 1),或者R+1(R < N),于是就可以递归求解了,递归出口为L=1,R=N的时候。
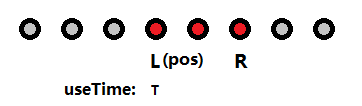
图2
如图,已经访问的宝物为红色标记的点,灰色标记的为未曾访问过的,并且现在的位置在已经访问区间的左端点L上,已经使用了T的时间,我们需要判断这个状态是否合法,则需要满足以下的几个不等式。
1、保证右边未访问的都能在截止时间内访问到:
T + (P[R] - P[L]) + (P[R+1] - P[R]) < D[R+1]
T + (P[R] - P[L]) + (P[R+2] - P[R]) < D[R+2]
...
T + (P[R] - P[L]) + (P[N] - P[R]) < D[N]
将这些等式化简,可得:
T - P[L] < D[R+1] - P[R+1]
T - P[L] < D[R+2] - P[R+2]
...
T - P[L] < D[N] - P[N]
再进行进一步化简,得:
T - P[L] < Min{ D[k] - P[k], R < k <= N }
2、保证左边未访问的都能在截止时间内访问到:
同理,可以得出:
T + P[R] < Min{ D[k] + P[k], 1 <= k < R }
那么,令 POSTM[i] = Min{ D[k] - P[k], i < k <= N }
PREM[i] = Min{ D[k] + P[k], 1 <= k < i }
这两个数组可以分别通过一次逆序和顺序的线性扫描求出来,用于搜索的时候判断可行性。例如,当T - P[L] >= POSTM[R] 表示在右边未访问的宝物中有至少一个宝物不能在截止时间前被访问到,T + P[R] >= PREM [R]表示在左边未访问的宝物中有至少一个宝物不能在截止时间前被访问到,直接剪枝。
还需要一个剪枝,就是在当前时间T加上当前状态下预计访问完所有宝物的最小时间已经比之前求出的最小时间大,直接剪枝。
H . Booklets
PKU 1968 http://poj.org/problem?id=1968
题意:N(N <= 3000)本小册子需要分配给S个学校,每个学校得到的是N/S的上整本册子或者N/S的下整本册子,每本册子有一个页数,并且规定分配册子的时候按照页数递增来分配,先把上整本册子分完再分下整的,对于每个学校的分书规则,按照输入的顺序进行分配。求问第T个学校分到的第一本册子的页数。
题解:需要求出几个量:
上整册子的数目UIP = (N+S-1) / S;
下整册子的数目LIP = N/S;
分到上整册子数目的学校个数UIPC = N % S;
分到下整册子数目的学校个数LIPC = N - N % S;
首先对所有的册子按页数递增来排序(如果页数相同按照下标递增排序),然后减去前T-1个学校的册子总数,容易得出第T个学校分到的册子数目C,从接下来的C个册子中找到之前下标最小的册子,它对应的页数就是答案。
I. Count on Canton
PKU 1969 http://poj.org/problem?id=1969
题意:给定下图所示的无限分数序列,并且按照蛇形方式编号,即第一个为1/1,第二个为1/2,第三个为2/1,第四个为3/1,以此类推,问第N个分数是什么。
1/1 1/2 1/3 1/4 1/5 ... 2/1 2/2 2/3 2/4 3/1 3/2 3/3 4/1 4/2 5/1题解:数学题。
首先二分求出在第几条斜线上,即(K-1)K/2 < N的最大的K,然后求根据K的奇偶性求出蛇形在第K条斜线的行走方向,第N - (K-1)K/2 个数就是答案。