SGU 120 - 129 解题报告
121 Bridges painting 图论:染色问题
122 The Book 图论:哈密尔顿回路
123 The Sum 递推
124 Broken Line 计算几何:线段判交
125 shtirlits 搜索:深度优先搜索
126 boxes 初等数论
127 Telephone directory 排序
128 Snake 排序 + HASH
129 Inheritance 计算几何:凸包+线段判交
120 Archipelago
计算几何:射线旋转
题意:需要求一个正多边形的N个点,但是给出的只有N和某两个点的坐标。
题解:核心思想是根据给定的那两个点的坐标确定多边形中心点的坐标,这样边长也确定了,然后利用中心点到其中一个点的射线的旋转求出所有的点坐标。
1) 正多边形的中心点一定在任意两个顶点的连线的中垂线上,然后根据已知点的相对关系,算出他们和中心点的夹角,利用这两个条件就可以求出中心点的坐标了。
2) 然后就是要求某个点绕中心点旋转360/N度后的坐标了,做N-1次旋转操作就能求出所有的顶点了。旋转可以通过解方程求解:
令原单位向量I,旋转alpha角度后的单位向量Ia,其中I和alpha已知,Ix是我们需要求的。那么有以下两个方程:
1) I.x * Ia.x + I.y * Ia.y = cos( alpha )
2) Ia.x2 + Ia.y2 = 1
将1)中的Ia.x用Ia.y表示代入方程2),利用一元二次求根公式可以求得两个解,然后算出Ia.x,但是解肯定只有一个,可以用叉乘关系排除掉另外一个解。
121 Bridges painting
图论:DFS构造
题意:对于一个图,给定它的边和点,现在要求给边染色(黑色或者白色)。问能不能构造一种染色方法,使得所有的度数大于1的点的边都能有至少有一条边为黑色、至少有一条边为白色。
题解:首先考虑什么情况下是不可能染色成功的;如图1所示,对于下面这个图,每个点的顶点度数为2,所以从任意一条边开始染色,相邻边必然为相反色,由于存在奇环,导致必然有一个点的两条边的颜色相同,染色失败。
然后再来考虑怎么将这个图挽救回来,其实这个图失败的点只有一个,如果在那个点上再加一条边,那么整个图貌似就可以认为染色成功了。
于是我们进一步考虑是不是度数为奇数的点造就了这一切:
度数 = 1,该点所在边可以随便染色;
度数 > 1,说明必然存在环;
如果是偶数环,那么经过一系列的交错染色,最后必然能够在该结点上收获两条颜色不一样的边;
如果是奇数环,在染色完毕后,必然还有一条边未被染色(因为度数为奇数),可以大胆的将它染成不同的颜色;
所以对于度数为奇数的点,采用交错染色,一定可以将图染色成功;
如图,可以对于所有奇度数顶点作为根进行一次dfs,按照编号顺序进行深度优先遍历,先遍历到的是1号,标记为黑色,然后将它的第一个儿子标记为白色,遍历完毕,将第二个儿子标记为黑色(交错染色),即每次更换结点的时候就将颜色取反,当我们遍历到边6的时候发现7是一条后向边,于是回到了根结点,完成遍历。
利用同样方法,将所有度数为奇数的点进行一次遍历,然后再将度数为偶数的点进行相同的遍历(因为可能这不是一个连通图,所以如果度数为偶数的点所在的图集合中有奇数环,如图1的情况,那么必然无解)。
遍历完毕,需要对每个点判断是否存在不合法的顶点(边数大于1,并且只有一种染色),如果合法,说明所有边都被染色了,输出解即可。
图1
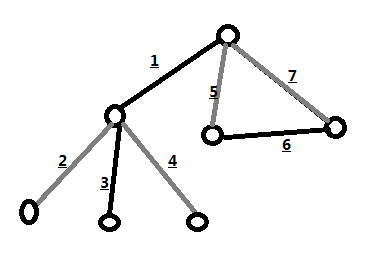
图2
哈密尔顿回路问题:Ore定理 + 构造
题意:给定N(N <= 1000)个点连成的图,每个点度数大于等于(N+1)/2,求这个图的一条哈密尔顿回路。
题解:
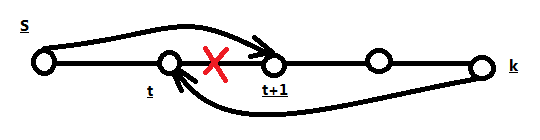
1)首先假设已经得到了一个环R(R的顶点个数为r),那么在未选到环内的点集R’中必然能够找到某个点k和环R中其中一个点j有边相连,假设没有边相连,那么环R和环外的点集R’互不连通,为两个连通分量,和题意相左(因为每个点的度数大于等于(N+1)/2,图论书上有证明,这肯定是一个连通图,故不再累述),故R’中必然存在至少一个点k和R中点j相连,于是将那个点j连接到k上,这样就变成了一个长度为r+1的链。
2)这个链的头为s,尾为k,长度为r+1,不断在剩下的点集中找点连接到s和k上,并且不断更新s和k(连接到头上,连接的点就变成了s,连接到尾上,连接的点就变成了k),直到找到一个极大连通子链(不能再在剩下的点中找到点连接到链的两端了)。
3)由于k和剩下点集R’没有点相连,所以我们只能在这条长链上找和k相连的点t(因为一定可以找到,为什么呢?k本身不就有个链内的点连着嘛,不然它就是个孤立点了)。所以找到(k , t)相连,并且(s, t+1) 相连,然后删掉(t, t+1)这条边,就能够得到一个新的环了,如果此时环的长度为n就结束了,否则继续1)。
123 The sum
递推
题意:求斐波那契数列的第N(N <= 40)项。
题解:__int64数组预处理即可。
124 Broken line
计算几何: 线段判交
题意:在平面上有一些闭合线段(没有自交和相互交叉),判断给定的点P是否在这个闭合线段内。
题解:其实就是判断一个点是否在多边形内;
首先,虚拟出一个无穷远的点Q,然后用PQ和每个闭合线段去做相交检测(两线段判交在黑书上有详尽的解释,不再累述)。
1) 如果P在某条线段上,输出BORDER;
2) 如果PQ和所有线段交点个数为奇数,说明在多边形内,输出INSIDE;
3) 如果PQ和所有线段交点个数为偶数,说明在多边形外,输出OUTSIDE;
125 Shtirlits
深度优先搜索 + 剪枝
题意:给定一个矩阵B (3X3),B[i][j]表示A[i][j]四周比它大的数的个数,求满足条件的A。
题解:枚举A[i][j]的每个数字,数字的范围为 [0,9]。复杂度109,所以需要进行一定的剪枝。
a) 首先,可以肯定这B[i][j]中一定会至少有一个0,因为总有一个数没有比它大的数(高处不胜寒啊~~)。对于B[i][j] == 0的格子,将A[i][j]设为最大值9一定不会错,所以复杂度至少可以降到 108 了。
b) 将A的每个非9的格子标记为-1,然后对每个格子进行枚举,枚举范围为 [ 0, 8 ], 因为B[i][j]为四周比它大的数的个数, 如果A[i][j]==9,那么B[i][j]必须为0,复杂度降至 98。
c) 每次枚举完毕,进入下一个数的枚举之前,进行全局的检测,对于每个格子统计以下数据:
i) 已经枚举的邻居格子 H
ii) 总共有多少个邻居格子 T
iii) 比自己大的邻居格子 B
然后进行筛选,如果
x) 比当前格子大的邻居数已经超出限定值, 即 B > B[i][j]
y) 比当前格子大的邻居数 + 剩余未知邻居数 < 给定比它大的邻居数, 即 B + (T-H) < B[i][j]
均为无效解,无需往下枚举,回溯。
d) 直到所有数枚举完毕,输出解即可。
126 Boxes
初等数论
题意:对于给定的A和B,
如果A > B, 则状态变为 (A-B, 2*B)
如果A < B, 则状态变为 (2*A, B-A)
当 A == B 时,结束。
要求输出这个情况是否存在,如果存在输出变换的次数,不存在输出-1。
题解:根据题意,可以得出一些简单的推论:
a) 当A == 0 或者 B == 0 时 答案为 0。
b) 最后A == B的时候,必定是K = (A+B)/2,所以当A+B为奇数时答案不存在。
c) 定义最后的状态二元组为 (K, K),
倒数第二次的操作必定为 (3K/2,K/2) 或者(K/2,3K/2) (2种)
倒数第三次的操作必定为 (7K/4, K/4) 或者 (3K/4, 5K/4) 或者 (5K/4, 3K/4) 或者 (K/4, 7K/4) (4种)
倒数第四次操作(15K/8,K/8)... (8种)
倒数第i次操作 ( (2(i-1)-1)/2(i-1) * K, 1/2(i-1) * K ) ... (2(i-1) 种)
d) A和B的组合必定在这些情况中找。
于是定义 A = L1 / 2n * K, B = L2 / 2n * K (其中K = (A+B)/2, L1,L2为奇数,并且(L1+L2) = 2(n+1))
得:
L1 = 2n * (A/K)
L2 = 2n * (B/K)
令 A = 2a * A', K = 2k * K'
则有 L1 = 2(n+a-k) * A'/K' 为奇数,所以n+a-k = 0,并且要保证A' mod K' == 0,A 和 K 都为已知,则可以计算出 a 、A'、k、K',最终的步数就是k-a+1。
需要注意特殊情况:A或B为0的情况,以及A+B为奇数的情况。
127 Telephone directory
将所有电话号码按首字母排序,统计每个首字母出现的次数Ai, Sum{ (Ai + K - 1 ) / K } + 2 就是答案。
128 Snake
想法题
题意:给定N(4<=N<=10000)个整数点,问能不能组出一个多边形,满足以下条件:
a) 闭合;
b) 所有的点都是多边形上的点,并且只能被用一次;
c) 任何两个连续的线段需要组成一个90度的直角;
d) 多边形的所有边都要平行于坐标轴;
e) 多边形不能存在自交;
f) 多边形的周长要满足最小;
题解:
1) 对于输入的点保存两份数组PX、PY,并且记录每个点在原数组的下标index;
2) 对PX进行X优先排序,对PY进行Y优先排序;
3) 对PX中序号为奇数的点PX[i]和它的下一个点PX[i+1]进行y值的判断,如果这两个点的y值不相等,那么说明这个点无法加入多边形中(PX[i]无法配对,被孤立了),无解。否则PX[i].index和PX[i+1].index必然有一条边(可以用邻接表来存边关系,因为最后求的是一个多边形,所以每个点有且仅有两条边,其实就是一个哈密尔顿回路)。
并且加PX[i+1].x - PX[i].index 累加到答案ans中;
4) 对PY中的点作和3)一样的处理,保存边的关系,但是这里需要判断一种自交的情况,如图1中,3)操作完毕后,产生三条边(1,1) - (2,1) (1,2) -(3, 2) (2,3) - (3,3);那么在进行操作4)的时候(1,1)-(1,2) 和 (3,2) - (3, 3)都是没问题的,唯独 (2,1) - (2,3) 和 先前的边 (1,2) -(3, 2) 会产生自交,违反了e这条规则,所以需要检测这种情况是否存在,如果存在,那么必然无解;具体检测方法很多,不再累述;
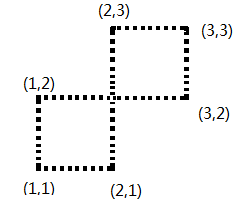
图1
5) 进过3)和4)后,再进行一次连通性判断即可,以防图2的情况。

图2
129 Inheritance
解析几何 + 凸包 + 线段判交
题意:给定一个多边形和若干线段,这个多边形内任意两点连线不会和多边形边界相交,分别求这些线段在多边形内部的长度。
题解:首先,根据“多边形内任意两点连线不会和多边形边界相交”可以肯定这是个凸多边形,于是问题就转化成了求某条线段和凸多边形相交后线段在多边形内部分的长度。
由于给定的点是乱序的,所以最简单的方法是求这些点集的一个凸包,构造出一个按点排序的多边形,相邻两点连线为原多边形的一条边。
那么枚举每条边和给定线段的相交情况:
1) 不相交(平行),继续判断下一条边;
2) 共线,直接跳出枚举,(由于是凸多边形,改线段肯定不可能在多边形内);
3) 相交,将这个交点存入集合S;
将原线段的两个端点存入集合S,对集合S的点进行x坐标递增排序(x相同时y坐标递增排序),然后枚举相邻两个点的中点,判断是否在在原多边形内,如果在,那么将这两个相邻点练成的线段的长度累加到最后的答案中。如图1为两个交点的情况。
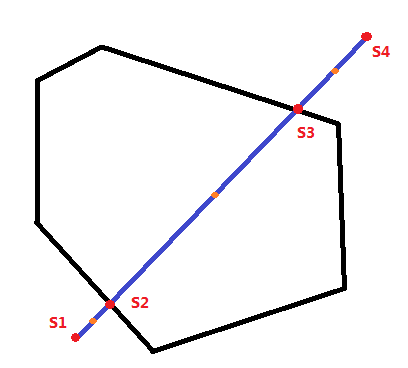
图1