SGU 110 - 119 解题报告
111 Very simple problem 二分枚举
112 a^b-b^a 二分求幂
113 Nearly prime numbers 数论:素数筛选
114 Telecasting station 枚举
115 Calendar 简单模拟
116 Index of super-prime 动态规划:记忆化搜索
117 Counting 二分求幂
118 Digital Root 数学题
119 Magic Pairs 数论:扩展欧几里得
110 Dungeon
计算几何:射线和球体相交
题意:给定一条3D射线 和 N个球体,问射线的各种反弹经过的球体编号,如果反射超过10次,只需要输出前十次。
题解:很明显,首先需要枚举每个球体和当前射线的相交情况,如果和多个球体相交肯定是取距离最近的球体进行相交计算,然后计算出空间反射射线,重复以上操作11次,如果某次的反射射线已经不能和任何球体相交那么直接跳出这个过程。
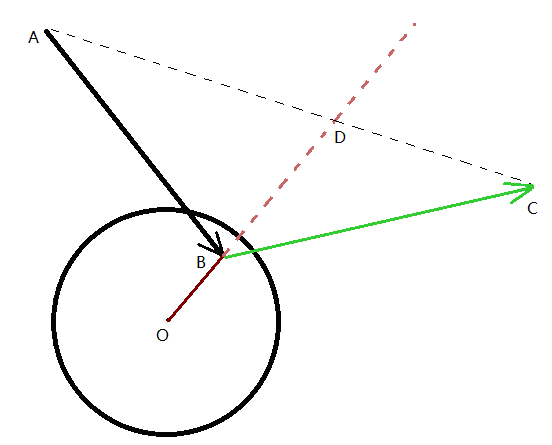
图1
如图1,表示射线AB和球O相交于B点,反射后的射线为BC,BD为球心O到交点的延长线,那么必定满足以下几个条件:
已知A点坐标(xa, ya, za),单位向量tab
B点坐标 为 (xb, yb, zb) = (xa, ya, za) + |AB| * tab (1)
B点在球O上,所以B点坐标满足
| (xb, yb, zb) - (xo, yo, zo) | = OB = Ro (2)
将(1)代入(2),可计算出|AB|的长度(由于是射线和球体求交,这两个方程求出来的是直线和球体的交点,所以还需要计算方向判断交点的可行性,如果交点有两个,则取距离小的那个,如果只有一个交点,说明是相切),然后利用(1)式计算出B点坐标。
2) 射线经过球体的反射射线
假设C点在A经过B点反射后的反射射线上,并且AB = BC,那么AC必定和OB延长线相交,假设交于D点;
单位向量cos(ABD) = Iba * Ibd;
BD = AB * cos(ABD);
向量AD = 向量AB + 向量BD;
向量AC = 2 * AD;
点C (xc, yc, zc) = 向量AC + (xa, ya, za);
向量BC求出后返回1) 继续判断和别的球的相交情况;
111 Very simple problem
二分答案 + 大数模拟
题意:给定X( X <= 10100),求X开方后的下取整。
题解:数组模拟大数。二分答案A,找满足 A*A <= X 最大的A即为答案。
112 a^b-b^a
二分求幂 + 大数模拟
题意:求 ab - ba ( 0 < a, b < 100)。
题解:数组模拟大数。二分求 AB。
当 B == 0 则 AB = 1; 否则 AB = (A2)(B/2) * ( (B mod 2) ? A : 1 ); 递归求解。
113 Nearly prime numbers
素数筛选 + 素数判定
题意:判断一个数是否为两个素数的积。
题解:利用传统的素数筛选将 1-31623 的素数筛选出来,31623为平方大于等于109的最小整数,因为一个数的开方内找不到一个(非1或它本身)因子的话它本身就是素数,所以素数只需要筛选到 109 的开方 即可。
对于每个数,遍历素数数组,如果能被某个素数整除,判断商是不是一个素数,如果商也是素数结果为Yes,否则为No。
114 Telecasting station
枚举 + 统计
题意:在X轴上规定一些有权值ai的点 (x1,a1), (x1,a1), (x2,a2) .. (xn,an)要求在x坐标上找到一个点X使得 M = |X-x1|*a1 + ... |X-xn|*an 的值最小。
题解:细心观察可以发现,M是关于X的一次函数,所以可以确定X必定为 x1...xn中的某个点。
由于原式中存在绝对值,为了将绝对值化简,可以将X的区间分段,比如当X 为 xj时可以简化为 M = (X-x1)*a1 + ...(X-xj)*aj + (xj+1-X)*aj+1 + ... + (xn-X)*an
= (X * presum[j] - preproduct[j]) + (postproduct[j+1] - X * postsum[j+1])
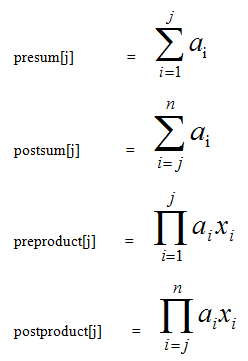
图2
这些辅助数组可以通过四次线性扫描得出,复杂度O(n)。然后,先将xi递增排序,枚举每个xi,计算最小值更新M,就可以在O(n)的时间内求解了。总体算法复杂度为排序复杂度O(n log n)。
115 Calendar
简单模拟
题意:给定一个月份M和天数N,求2001的那一天是星期几。
题解:可以预处理出每个月的天数,如果天数大于那个月对应的天数或者月数大于12肯定是不可行的,否则将给定月数M之前的 1到M-1个月的天数相加再加上N得到Sum,Sum mod 7就可以定位到星期几了。
素数筛选 + 记忆化搜索(或 动态规划)
题意:超级素数是素数下标也是素数的数,给定一个数N,问这个数能不能被一些超级素数组合出来,如果可以,需要满足超级素数的个数最少,要求输出一个方案。
题解:先将满足条件的 超级素数 筛选出来,3 5 11 17等等,然后对于输入的N进行一次记忆化搜索(DP)
例如 N = 15
那么N的最优值一定是来自 15-3=12, 15-5=10, 15-11=4 这三个数,以此类推,递归出口是N = 0,每次计算完N就将它保存下来,下次就不用重复计算了。
所以状态转移方程为:DP[i] = min{ DP [ i - p ] , p 为超级素数 } + 1
因为需要输出组合的序列,所以每次搜索,需要保存当前最优值的前驱结点,最后一次性输出即可。
117 Counting
二分求余
题意:给定N(N < 10001)个数Ai,求其中AiM 是K的倍数的数的个数。
题解:对于ab mod c二分求解。当 b == 0 则 ab mod c = 1 mod c; 否则 ab mod c = (A2)(B/2) * ( (B%2) ? A : 1 ) mod c;
118 Digital Root
数学归纳法
题意:定义f(n) 为 n的所有数字的和. 如果 f(n) 是1位数字,那么它是n的 "digital root",否则n的"digital root" 为 f(n) 的"digital root"。
给定数组Ai,求 A1*A2* … *AN + A1*A2*…*AN-1 + … + A1*A2 + A1 的"digital root"(N <= 1000)。
题解:定义d(n)为n的"digital root",利用数学归纳法可证明(从N=1的情况网上递推):
1) d( A1*A2* … *AN ) = d( AN * d( A1*A2* … *AN-1 ) )
2) d(A1 + A2 ) = d( d(A1) +d(A2) )
利用这两点,可以直接扫描A数组就可以计算出给定表达式的"digital root"了。
119 Magic Pairs
枚举 + 扩展欧几里得
题意:对于所有的(X,Y)在满足 (A0 * X + B0 * Y) % N = 0 (1) 的情况下,使得(A * X + B * Y) % N = 0 (2) 也成立, 求这样的 (A, B)。
题解:首先求出A0、B0、N三者的GCD,最后算出来的答案需要乘上这个GCD。
(A0 * X + B0 * Y) = K * N (3) (K为整数)
(A * X + B * Y) = K' * N (4) (K'为整数)
X = (K*N - B0*Y) / A0
代入(4)式,可得
A*(K*N - B0*Y) + B*A0*Y = K'* N * A0 (5)
化简得 (6)
(B*A0 - A*B0) * Y = (K'*A0 - K*A) * N (6)
两边同时mod N
得 (B*A0 - A*B0) * Y % N = 0 (7)
由于Y为任意整数(即Y有可能和N互素), 所以必须满足 (B*A0 - A*B0) % N = 0 (8)
可以化简为 (B*A0 - A*B0) = K'' * N (9) (K''为整数)
A0 * B + N * (-K'') = A*B0 (10)
枚举A的值,就可以把方程转化成了 ax + by = c的形式,其中:
a = A0, b = N, c = A*B0
x = B, y = -K''
利用扩展欧几里得即可求得最小的满足条件的x(即B)的值了。
最后的答案需要乘上 A0、B0、N 三者的GCD。