Mid-Central USA 2009 解题报告
PKU 3912 http://poj.org/problem?id=3912
题意:给定一个一维的棋盘,范围为[0, W] (W <= 1000,000,000),某两个点之间有梯子或虫洞,梯子的下端点到上端点以及虫洞的上端点到下端点花费的步数为0,其它任意点之间的距离通过跳跃来计算,最多每次跳跃不超过S格(S<= 6),跳跃的过程中如果跳到梯子的下端点或者虫洞的上端点就会被直接传送到另一端,并且每次跳跃只能从小的点跳到大的点(虫洞是个例外),求从0到W的最短距离。
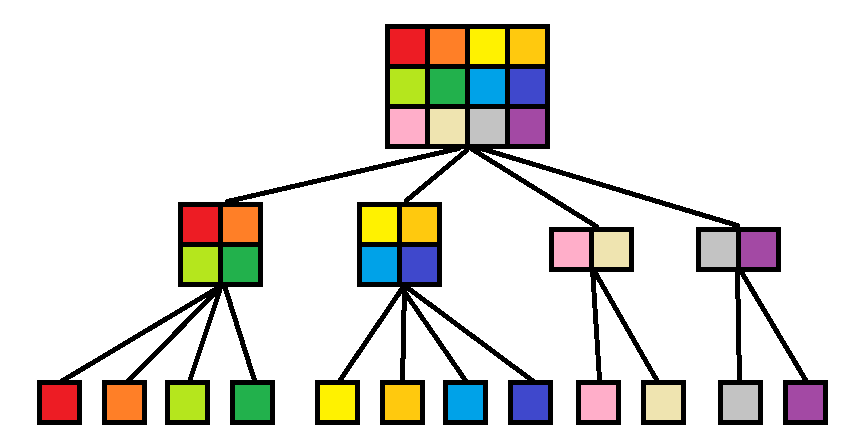
图A-1
题解:
离散化 + SPFA。
将所有梯子和虫洞的两端点、0和W以及他们往前往后S步以内的数全部记录下来,梯子和虫洞有P(P <= 40)个,加上起点终点,总共82个点,算上前后各六步,总共82 * 13 = 1066个点,然后将这些点排序后离散化,最后就是要构建一个网络图,通过网络求0到W的最短路,最短路可以用SPFA求解。
谈谈建图的过程,对于任意两个点,他们之间必定可以连一条边,然后有一个步数表示边的权值(这里的步数也可能是正无穷,也即永远都无法到达)。
对于任意两个点(u, v),他们的步数w(u, v)(边权)我们做如下讨论(这里的u、v是离散化后的点):
1)如果u是梯子的下端点,v是梯子的上端点 或者 u是虫洞的上端点,v是虫洞的下端点,那么w(u, v) = 0,否则进入2)的判断;
2)如果u的编号大于v,w(u, v) = inf,表示永远不可达,因为某次跳跃只能从小的点跳到大的点,否则进入3)的判断;
3)如果u的实际位置和v的实际位置差值小于等于S,则w(u, v) = 1;
4)检查u和v之间是否有虫洞的上端点或者梯子的下端点,之后将这两种点称为X点
a)如果有,判断他们是否连续,
i) 如果不连续w(u, v) = inf(这一步这么做是为了简单化,试想一下,如果X点不是全部连续,说明u可以先跳到他们中间的某个非X的点,然后再跳到v点,这一步是通过SPFA来实现迭代的,建边的时候可以不考虑)。
ii)如果连续,判断他们连续的格子的数目,如果大于等于S说明这个连续的块必定跳不过去,所以w(u, v) = inf,否则可以先跳到最先的一个X点的前面一个点,然后经过一步S跳跃将这个连续块跳过去,再跳到v。
b)如果没有X点,那么直接从u点跳到v点。
这里我们需要计算从a点跳到b点不考虑虫洞和梯子的最短距离,可以贪心的跳,每次往大的跳,直到剩余格子不足S格,即(b-a + S-1) / S (b-a对S求商的上整)。
边建立完成就可以利用广搜求解0-W的最短路了。
B. Gnome Sequencing
PKU 3913 http://poj.org/problem?id=3913
水题,判断三个数是全递增还是全递减还是无序。
C. DuLL
PKU 3914 http://poj.org/problem?id=3914
题意:给定一些dll文件和它占用的内存空间,以及一些可执行程序占用的内存空间和它依赖的dll文件,程序以进程为单位,两个相同的程序可能有不同的进程,进行一些下列的操作:
1)某个程序运行的时候需要它依赖的dll文件也加载到内存中,多个程序可以共用一个dll文件;
2)某个程序退出的时候,如果它所依赖的dll文件没有其它程序使用,需要释放这段内存空间;
给定一系列的运行进程,求某个时刻的最大内存占用。
题解:HASH的简单应用。
初始化内存占用V = 0,
对于给定的输入进程:
1)如果是新运行的进程,将V加上这个进程的内存占用,并将它所有依赖的dll文件检查一遍,如果引用计数为0,则将对应dll文件的内存累加到V上,引用计数+1;
2)如果是退出进程,将V减去这个进程的内存占用,并将它所有依赖的dll文件检查一遍,如果引用计数为1,则用V减去对应dll文件的占用量,引用计数-1;
每次操作记录最大的V就是最后的答案。
D. Black Vienna
PKU 3915 http://poj.org/problem?id=3915
题意:三个人,每个人五张牌,互相不知道对方的牌,还有额外的三张牌放在一边(所有牌编号为A - R)。每一轮,由 (i-1)%3+1 (1 <= i <= 15) 号玩家进行发问,问Ai (1 <= Ai <= 3) 号玩家XYZ(代表任意三个牌号)三张牌中有多少张在他手上,然后他回答Bi (0 <= Bi <= 3),问经过多少轮之后有某位玩家知道 额外 的那三张牌是什么。
题解:dfs枚举 + 剪枝。
首先枚举到某个询问i的时候玩家j能够猜出的那三张牌的情况,如果枚举完所有情况最后确定只有一个解满足条件的时候,那个询问的编号i就是答案了。
类似IDA*的思路,先枚举询问最大深度,如果到达那个询问不能确定额外的那三张牌或者有很多种情况,那么说明还需要更多的询问,迭代深度继续枚举。
对于某个询问i,找到询问的那三张牌中已经是Ai号选手的数量ansCnt,以及尚未确定牌的归属的牌的数量xCnt,如果已经确定位置的牌数量 大于 实际他回答的数量(ansCnt > Bi)或者 尚未确定位置的牌数量 + 已经确定为他的牌数量 小于 实际他回答的数量(ansCnt + xCnt < Bi)都是不合理的情况,剪枝,不用继续往下搜索;
否则,将(Bi - ansCnt)张牌分配给Ai,(xCnt - (Bi - ansCnt))张牌分配给其它两位玩家以及额外的那一堆,这里需要用到嵌套dfs枚举,枚举完后进入下一个询问的枚举,每次询问的时候可以有几个剪枝:
1)如果某个阶段某个人的牌数超过5张;
2)枚举的解的数量超过2个;
3) 对于一次完全枚举,枚举完所有询问后还是有无法确定三张额外的牌的情况;
E. Duplicate Removal
PKU 3916 http://poj.org/problem?id=3916
水题,对输入的元素进行连续判重输出。
F. Rock, Paper, Scissors
PKU 3917 http://poj.org/problem?id=3917
水题,剪刀石头布!O_o
G. A to Z Numerals
PKU 3918 http://poj.org/problem?id=3918
题意:复杂模拟。(没做出来,#-_-# 样例的98是怎么出来的呀!!!)
H. Cell Towers
PKU 3919 http://poj.org/problem?id=3919
题意:给出一条曲折的连续线段,曲线从起点开始每经过一个长度为1的单位会放置一个守卫K,在曲线以外的某些地方会有T(T <= 10)个信号发射器,用A、B、C...来表示,每个信号发射器有它的信号强度Pi,每个信号发射器到守卫K的距离如果是D,那么它能接收到的信号值为Pi / D2的最近整数,并且对于守卫K,它只会接收最大的信号值,如果有多个发射器对于K的信号值相同,那么选择字典序最小的发射器。需要求是一些守卫集合,这些守卫分别和它的前一个守卫所接收的信号发射器不一样。
题解:计算几何、向量的简单应用。
对于每条射线,终点减去起点,再单位化后就可以得到这条射线的单位向量,利用这一点可以很简单的将所有守卫的坐标求出来,然后对于每个守卫判断接收的是哪个发射器,判断和之前那个守卫是否相同即可。
需要注意的是最后一个守卫,当和上一个守卫距离小于0.5的时候不会建立新的守卫。
I. RIPOFF
PKU 3920 http://poj.org/problem?id=3920
题意:给定N(N <= 200)个数的一维数组A,取不大于T+2个数,每相邻两个数之间的下标不大于S,问最大的取值总和(第0个和第N+1个数必取,且权值为0)。
题解:动态规划。
DP[i][j] 表示第j个数取 A[i]的最大值,那么状态转移方程可以表示为:
DP[i][j] = max{ DP[k][j-1] + A[i], i > k > i-1-S && k >= 0};
特殊的,DP[0][0] = 0,其他的DP[i][j] 都初始化为INF;
最后计算出的DP[N+1][i]中的最大值就是答案了。