South America 2002 解题报告
PKU 1290 http://poj.org/problem?id=1290
题意:给定一个3X3的六面魔方(每个面有3X3个块),求经过某些旋转之后能否使得所有面的颜色都相同,旋转包括对某个面进行顺时针和逆时针旋转(共12种情况)。
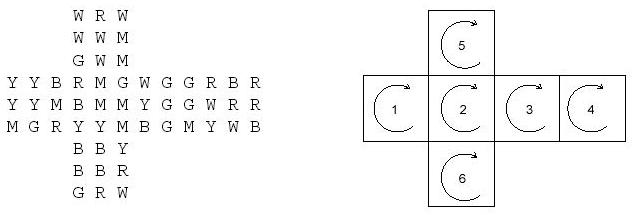
图A-1
如图1,输入数据为左图的形式,右图给对应的面编号,箭头方向为顺时针旋转方向。
+A表示对A这个面进行一次顺时针旋转,-B表示对B这个面进行一次逆时针旋转。问经过一定的+A/-B操作之后能否使得所有面的3X3个字母都相同。
题解:模拟题
做法很多,这里介绍一种比较容易理解的状态记录方式,考虑某次旋转,一定是旋转某个面,然后对邻接的四个面的某条边进行顺次平移。如图A-2, 2号面的旋转带动的是1、5、3、6四个面。
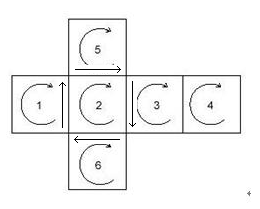
图A-2
我用一个数组rotate_n来记录某个面旋转的时候带动的面的编号集合(编号为0的数据为占位符),那么有:
int rotate_n [7][4] = {
{0, 0, 0, 0}, {4, 5, 2, 6}, {1, 5, 3, 6}, {2, 5, 4, 6}, {3, 5, 1, 6}, {1, 4, 3, 2}, {1, 2, 3, 4}
};
光记录带动的面是哪些还不够,还需要知道带动面的对应边,对于一个魔方的一个面,我们编号如下:
(0,0)(0,1)(0,2)
(1,0)(1,1)(1,2)
(2,0)(2,1)(2,2)
分别用1到4来代表一个面的四条边(注意,有方向):
1 (0,2) - (0,0)
2 (2,2) - (0,2)
3 (2,0) - (2,2)
4 (0,0) - (2,0)
那么同样用rotate_p来记录某个面旋转的时候带动的面对应的边,则有:
int rotate_p[7][4] = {
{0, 0, 0, 0}, {2, 4, 4, 4}, {2, 3, 4, 1}, {2, 2, 4, 2}, {2, 1, 4, 3}, {1, 1, 1, 1}, {3, 3, 3, 3},
};
这样一来,我们只需要考虑一个面的旋转,然后套用对应的数据即可,还有一个比较巧妙的是,逆时针旋转不需要特殊处理,直接将顺时针旋转执行三次即可。
B.This Sentence is False
PKU 1291 http://poj.org/problem?id=1291
题意:给定一些句子形如“Sentence X is true/false”的句子,X表示第几个句子,问所有的情况是否合法,如果合法,输出最大的可能为真的句子。
题解:2-sat。
每个句子抽象成两个结点,为真的时候为X,为假的时候为X '。
a) 对于第X个句子,如果是 Sentence Y is true;
则这个句子为真的时候, X ->Y连边;
当这个句子为假的时候,X ' -> Y '连边;
b) 对于第X个句子,如果是 Sentence Y is false;
则这个句子为真的时候, X ->Y '连边;
当这个句子为假的时候,X ' -> Y连边;
然后求一次强连通,如果最后有某个点X和X ' 在同一个连通图中,说明逻辑错误,说明必然存在不合法的情况,否则对于每个连通分量,求出为真的点的个数和为假的点的个数,然后将他们之中的大者累加,最后答案除2就是最大的可能为真的句子(除2的原因是因为真假是对称的)。
C.Will Indiana Jones Get There?
PKU 1292 http://poj.org/problem?id=1292
题意:营救公主,营救路线要么绕着墙走,要么走两面墙的最短距离(这种情况下需要在两面墙之间搭一块木板,并且可以反复使用)。问营救过程中木板的最短长度。
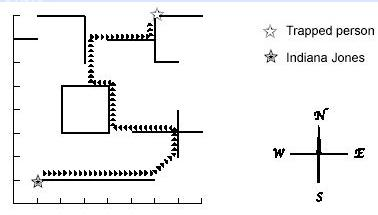
图C-1
题解:线段距离 + 二分答案
因为木板可以反复使用,所以我们可以假设如果木板越长,能够营救公主的概率就越大,反之则越小,所以问题就是求满足两点可达的最小木板长度,可以二分枚举这个长度T,如果两面墙的最短距离大于这个T,表明两面墙不可达,将墙抽象成点,两面墙之间的最短距离可以通过线段和线段的最短距离预处理出来,然后每次二分答案后通过一次搜索就可以找出起点和终点是否可达,复杂度为O(n^2)即计算两线段距离时候的复杂度。
D. Duty Free Shop
PKU 1293 http://poj.org/problem?id=1293
题意:给定M(M <= 1000)个白巧克力和L(L<= 1000)个黑巧克力,然后给定N(N <= M + L)个容量为Ci的盒子,问能否找到一种方案,使得某些盒子放满白巧克力,剩下的盒子放满黑巧克力。
题解:背包问题。
由于需要将每个盒子都放满,于是可以利用一维背包的求法将Ci的所有小于等于M的可行组合求出来,找到最大的M ' <= M,并且M ' 能够通过某种方式被组合出来,那么所有盒子的容量Sum 减去 M ' 的差小于等于L的话,必定能将剩下的盒子填满黑巧克力,否则无解。
这题需要记录前驱,并且注意M = 0 以及 L = 0 的情况(主要是在输入的时候判断退出条件,M+L==0退出而并非 (M&&L;) == 0)。
E.Not Too Convex Hull
PKU 1294 http://poj.org/problem?id=1294
题意:给定N(N<=101)个点(没有三点共线的情况),要求用B(B<=50)根皮条将这N个点圈成B个部分,每个部分为一个凸多边形,并且所有凸多边形公用一个点(这个点会给出),求众多方案中满足所有多边形面积和最小的方案。图E-1表示用两根皮条圈住19个点的情况(原点共用了两次)。
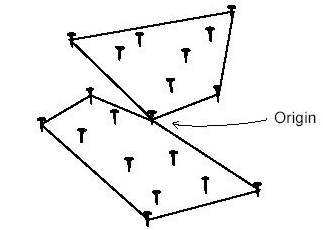
图E-1
题解:环形动态规划。
首先将所有点按照给定的原点进行极坐标排序,那么第1个点到第N个点必定是按照极坐标严格逆时针排布的(因为没有三点共线),用DP[i][b]表示第i个点到第N个点经过b次分割后分割完的凸多边形的面积总和最小值,那么:
DP[i][b] =min{ area[i][k] +DP[k+1][b-1] (i < k < N) }; 特殊的,DP[0][0] = 0;
area[i][j] 表示极坐标在第i个点和第j个点之间的所有点(包含这两个点)加上原点组成的凸包的面积,可以通过初始化预处理出来;
由于点是极坐标排列的,也就是第一个点不一定是凸包边上的点(有可能是第N-1个点到第2个点组成的凸包达到整体最优),所以需要做N次DP,可以将所有点复制一份,枚举起点i ( 1 <= i <= N),终点即i+N, 然后分别做一次DP取最小值。
时间复杂度O(N^2 * B)。
F.I hate SPAM, but some people love it
PKU 1295 http://poj.org/problem?id=1295
题意:N(N<=20)个人互发邮件,某个人收到邮件后一定会回复给他所有的好友,回复的数量决定他的称号,按顺序给定首先发起邮件的人,要求按顺序输出所有人得到的称号。
题解:深搜枚举。
数据量很小,对于给定的初始者作为起点进行遍历,每个人只访问一次,访问到的时候根据他的朋友数量计算他的称号即可。
G.Noise Effect
PKU 1296 http://poj.org/problem?id=1296
题意:给定两个正方形矩阵,求他们的最大相似度,相似度的定义为矩阵元素对应位差值小于等于100的个数占所有矩阵元素的百分比(可以进行旋转和翻转)。
题解:模拟题。
每个矩阵可以进行四次旋转,每次旋转可以有水平翻转、竖直翻转、水平竖直翻转、保持原样四种状态,一共十六种情况(实际小于16种,因为有些状态经过翻转和旋转之后是一样的),对每种情况模拟计算相似度取最大值即可。
H.Supermarket
PKU 1297 http://poj.org/problem?id=1297
题意:约翰需要买M(M<=100)件物品,超级市场上的物品都排成一排,一共N(N<=100000)件物品,他从左向右开始选物品,但是为了不麻烦,不想走回头路,而且第i个物品买的条件是,前i-1个物品必须已经买了,但是每个物品在超级市场中的价格不一样,即使同一个物品也有不同的价格,为了花费最少,他想要一个方案使得:
1) 按顺序购买M个物品;
2) 总价值最少,并输出这个最小值,如果方案不存在,输出Impossible。
题解:动态规划。
DP[i][j]表示第i个购买列表中的物品和第j个市场中的物品匹配时的最小消费(1<=i<=M,1<=j<=N);
Min[i][j]表示min{ DP [i][x] x<=j };
a)当第i个物品和第j个市场物品编号相同时,DP[i][j] = Min[i-1][j-1] +cost[j];
b)否则DP[i][j] = inf; 计算DP数组同时更新Min数组,由于每次的状态最多和上一行有关,所以在进行状态转移的时候可以采用滚动数组。时间复杂度O(NM)。