如何制作水球动画图?
起因
在 echart 的 Issue 上看到有人有水球百分比可视图的需求, 并且在 pull-request 上看到有人有类似实现,但是却感觉实现的并不完美,于是想自己尝试实现。
样式
思路
主要的核心代码还是水波动画的构建,这里我使用的是 Sin() 图像模拟的方法。
只要对 Sin() 函数进行一定的变形 (如: Sin(0.5 * (X+0.07))) 就能够模拟出类似的水波效果。如何实现动画呢?
只要设定一个周期变量,每一帧不断平移周期 就能模拟出水波运动的效果,最后使用 ctx.clip
使用 绘制好的圆路径对水波进行裁切,就能得到最终的结果。
数学基础
这里设计到一些中学学到的知识,一起回忆一下。
请允许我盗一张图:
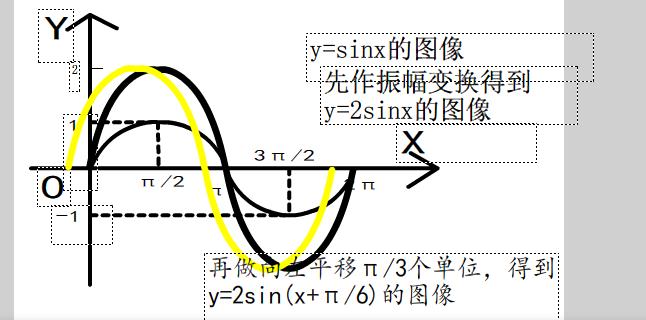
上图中展现了 从 Sin(X) -> 2Sin(X + PI / 6) 的情况。
我们可以看到,如果对 Sin(X) 乘以 一个大于1的系数(2)函数的振幅会变得陡峭,反之 如果乘以一个小于1的系数 函数的振幅则会变得平坦 所以我们称 这个系数为 振幅。
如果对 自变量X 加上 系数 PI/6 那么函数就会向左移,反之如果减去 某一系数 则会向又移动 , 我们称这个系数为偏移量。
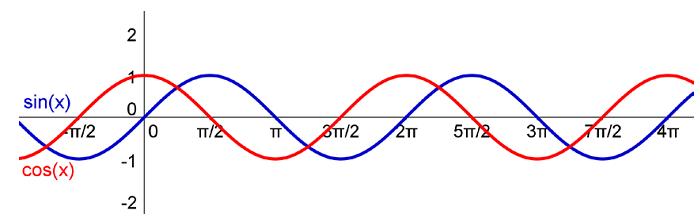
如图展示了 sin() 和 cos() 的图像,可以发现 他们是有规律的 无限函数,并且以一定周期 往复循环,所以我们 将 从 0 到 2*PI 成为一个周期。
模拟水波
首先我们尝试一下画出一个标准的Sin()曲线:
<canvas id="c"></canvas>
JavaScript
canvas = document.getElementById("c");
ctx = canvas.getContext("2d");
// 初始化Math 函数集
M = Math;
Sin = M.sin;
PI = M.PI;
Round = M.round;
// 设置画布宽和高
oW = canvas.width = 800;
oH = canvas.height = 300;
// 曲线起始点坐标
sx = 0;
dy = oH / 2;
axisLength = 800; // Sin 图形长度
xoffset = 0 // x 偏移量
unit = axisLength / 8; // 波浪宽
function drawSine () {
var points = []
x = 0
y = -Sin(x);
// 细心的同学可以发现 为什么这里Sin需要乘以一个负数。
// 这是因为 我们数学研究的直角坐标系和 浏览器的坐标系不同
// 浏览器的坐标系 相当于 平时研究的坐标系的第四象限, 所以为了得到标准的 Sin 函数我们需要取负
ctx.beginPath();
ctx.moveTo(xoffset, dy + y * unit);
// axisLength 设定是 可视区的宽度,xoffset 即上文提到的偏移量,20/axisLength 即 每 20/axisLength 取一个轨迹点
// 如果需要让轨迹点更加密集, 则可以将20 替换为 10 5 甚至 1
for(var i = xoffset; i< xoffset + axisLength; i+=20/axisLength) {
x = (xoffset + i) / unit;
y = -Sin(x);
// 记录轨迹点
points.push([i, unit * y + dy]);
ctx.lineTo(i, unit * y + dy);
}
// 获取起点坐标和终点坐标
var s = points.shift();
var e = points.pop()
ctx.lineTo(e[0], oH);
ctx.lineTo(sx, oH);
ctx.lineTo(s[0],s[1])
ctx.strokeStyle = "#00f"
ctx.stroke();
}
drawSine();
 ;
;
控制水波起伏
然后让我们 给画好的图形添加一定的振幅:
y = -Sin(x) * 0.5;

可以发现 我们可以通过控制振幅 来模拟水波的起伏
添加运动效果
曲线绘制好了,怎么让其动起来呢?
这时候,上文提到的 周期 就派上用处了,只要x + 从一定的周期偏移 就能不断的改变我们看到的曲线:
sp = 0; // 添加一个周期变量
// 设置一个渲染函数
function render () {
ctx.clearRect(0, 0, oW, oH);
sp += 0.03; // 循环中不断的改变该偏移量
drawSine(sp);
requestAnimationFrame(render)
}
X + 偏移量:
...
x = sp // 起始点改为 偏移量
y = -Sin(x);
ctx.beginPath();
ctx.moveTo(xoffset, dy + y * unit);
for(var i = xoffset; i< xoffset + axisLength; i+=20/axisLength) {
x = sp + (xoffset + i) / unit; // 每个轨迹点都添加上偏移量
...
这时候我们就可以得到一个运动的水波动画:

比例控制
我们需要对水波的高低进行控制,控制的参数就是 传入的数据百分比 。重点是找好 比例和 高度的逻辑关系 然后控制 y 点坐标值就ok 了:
var dy = 2*cR*(1-nowdata) + (r - cR) - (unit * y);
圆形裁切
我们这时候使用clip 将不想展示的部分裁切掉,就可以得到一个圆形的水波轮廓:
ctx.beginPath();
ctx.save();
ctx.arc(x,y, R, 0, 2*PI, 1);
ctx.restore()
ctx.clip();
其他补充
例如开场的圆形绘制动画,思路根据圆的参数方程 获取轨迹点,渲染的时候挨个点进行绘制连线。水波振幅的控制(85-90 水波需要平缓一些)。还有range组件的控制就不细说了,相信聪明的你通过剖析源码,定能明白里面的玄机。
源代码
需要源代码的同学可以在这里 下载到源码
喜欢该效果的朋友可以不要吝惜您的star哦~
如需转载,烦请注明出处:http://www.w3cplus.com/animations/water-bubble.html