浅说深度学习(2):简史
深度学习简史
第一个貌似深度学习的、具有多层非线性特征的算法可以追溯到1965年,Ivakhnenko和Lapa 用多项式激励函数组了个模型(图1),不宽但还挺深,结合统计方法做分析。在每一层里都用统计方法选择出最好的特征,并前馈给下一层。他们并没有使用反向传播来端到端地训练网络,而是逐层使用最小二乘法单独拟合。

图1:已知的第一个深层网络架构,由Alexey Grigorevich Ivakhnenko在1965年训练。每层之后的特征选择都导向更窄的架构,当再也加不上别的层的时候,网络优化也中止了。Image of Prof. Alexey Ivakhnenko courtesy of Wikipedia.
1979年,Fukushima最早使用了卷积网络。Fukushima的网络有多个卷积核池化层,这跟现代网络很像,只不过Fukushima的网络是用一种增强格式训练的:一溜激励函数随着时间逐步增强。另外还可以手动增加某些连接的权重,以指定重要的特征。 此时,用于训练深度模型的误差反向传播还没有诞生。早在1960年代,反向传播就已经被推导出来了,但是形式因为不尽完善,效率还太低。现代的反向传播形式是Linnainmaa在他1970年发表的硕士论文中推到的,还包含了Fortran代码,不过没有提到在神经网络中的应用。至此,反向传播还是默默无闻,到80年代早期还是仅有极少成型的应用。直到1985年,Rumelhart, Hinton和Williams指出反向传播在神经网络中可以形成很有趣的分布式表征。这是认知心理学的一大突破,此前一直有个争议,即人类的识别是基于分布式表征(联结主义),还是符号逻辑(计算主义)。
反向传播算法首个真正实用的应用来自LeCun于1989年在贝尔实验室的成果。他是用卷积网络和反向传播来对手写数字(MNIST)进行分类,该系统之后在美国被用于识读大量的数字检查。上面的视频里,93年Yann LeCun在展示如何用LeNet网络识别并分类数字。 尽管有如此多的成功,投入的科研经费仍然很稀少。“AI寒冬”期间,“人工智能”甚至沦落成伪科学代名词。但很多重要进展也正是出现在这段时期,比如1997年Schimidhuber研发出循环神经网络的长短期记忆(LSTM),不过彼时其表现还是不如95年Cortes和Vapnik开发的支持向量机,所以不被重视。
下一个重大的转折,发生在电脑速度的进一步提高,特别是GPU的引入,在过去10年里将计算速度提高了1000倍。此时神经网络已经逐渐匹敌支持向量机,虽然速度稍慢,但是在同等数量的数据上,已经能够取得更佳的结果。不像其他简单算法,神经网络随着训练数据增多,是持续攀升的。
这时的主要困难在于如何训练庞大、深层的网络,因为它正面临梯度消失问题:前面几层的特征无法被学得,因为学习信号不能返回这些层。
第一个解决方案就是逐层预训练:模型在每个层中以无监督学习的方式训练,这样前面几层的特征就经过了初始化或“预训练”,从而获得还不错的特征(权重)。前几层的特征只需要经过有监督学习微调,就可以达到不错的结果。第一个面向循环神经网络的预训练方法由Schmidhuber在1992年发明,Hinton和Salakhutdinov在2006年移植到了前馈网络上。另一个针对梯度消失的方案是97年的长短期记忆(LSTM)。
随着GPU速度的迅猛提升,不用预训练也可以训练出深层网络,比如卷积网络了。2011、2012两年,Ciresan和他的同事们,用卷积网络架构赢得了人物识别、交通标示识别和医学影像识别等比赛,也证明了这一点。Krizhevsky,Sutskever和Hinton在2012年用了类似的架构,还结合了修正线性激励函数,还用Dropout做正则化。他们在ILSVRC-2012 ImageNet竞赛上斩获了优异成绩,昭示着“特征工程已死、特征学习当立”。Google, Facebook, Microsoft注意到了这一大趋势,与2012年至2014年并购了大批深度学习创业公司和研究团队。从此,深度学习研究进入了快车道。
延伸阅读: Deep Learning in Neural Networks: An Overview
感知机
感知机只含一个线性或非线性单元。从几何学上讲,经过Delta规则训练的非线性感知机,可以找到分离两类数据点的非线性平面(如果该平面存在的话)。如果没有这样的平面,感知机也会生成一个准确度最佳的分离平面。感知机的优秀表现,带来了人工智能的一阵浮夸风。然而在1969年,却发现感知机会在一些看起来很简单的模式上失效,比如XOR(亦或)函数。感知机的失败是第一次AI寒冬的重要原因。尽管含有隐藏层的神经网络,并没有感知机的这些典型问题,但总是和感知机联系到一起,而且在AI寒冬期间,神经网络也遇到了图像问题。
尽管如此,纵然深度学习已经相当成功,感知机在大数据领域仍有一席之地,因为其简单的特性,是超大数据集上的应用变得轻便可行。
AI寒冬
机器学习和其他解释方法的快速发展,使很多人对人工智能盲目乐观(今天仍有类似声音)。研究者承诺这样的大跃进会持续存在,并终将带来强人工智能,于是得到了大量的资金投入。
到了1970年,显然这样的承诺是无法兑现的,金主争先撤资,人工智能跌下神坛与伪科学为伍。研究变得十分困难(没有经费;成果发表通不过同行评审),但仍有一小撮然研究者负重前行,终于带来了AI中兴,始有今日的深度学习盛举。
过犹不及,深度学习的泡沫是危险的,明智的研究者会避免预测未来——因为他们不想遇到下一个AI寒冬。
AlexNet
AlexNet是根据Alex Krizhevsky命名的卷积网络架构。Alex和Ilya Sutskever,在Geoffery Hinton的指导下,将这套架构应用在ILSVRC-2012竞赛的ImageNet数据集上。他们改进了Ciresan等人的架构,后者使用修正线性单元加速以及Dropout提高泛化能力,赢下了2011-2012年多项世界级竞赛。他们的结果与特征工程方法迥然不同,确立了深度学习在计算机视觉界的领先地位。AlexNet预示着深度学习技术即将成为主流,当然也有深度学习泡沫的隐患。
延伸阅读:ImageNet Classification with Deep Convolutional Neural Networks
训练深度学习架构
训练
训练深度学习架构,就像教小孩儿认识世界。当小孩儿见到一个新的动物,比如猴子,他们不知此为何物。这时候大人就指着猴子说:“这是猴子”,然后小孩儿就会把他们所见的画面和“猴子”这个标签联系起来。
单一张图片还是不足以教会孩子正确识别猴子,他们可能会把树懒当成猴子(或反之),甚至干脆忘记了动物的名字。为了建立可靠地记忆和识别,孩子们需要观察很多不同的猴子以及相似的动物,并且每次都要知道那到底是不是猴子——反馈对于学习是必不可少的。经过一段时间,如果孩子们见过了足够多的动物+名字,他们就能区分不同的动物了。 深度学习过程类似。我们把猴子照片给神经网络,深度神经网络会预测一个输出,比如图中物体的标签(“猴子”)。之后我们再给网络提供反馈,比如30%概率是猴子、70%是树懒,猜树懒的这部分输出是错的,我们就用这一误差来调整神经网络的参数,而调整方式就是,反向传播算法。
通常我们随机初始化深度网络的参数,这样网络也会产生随机的输出。这意味着对于内有1000个分类的ImageNet,我们的分类准确率就是0.1%。为了提升性能,我们需要调整参数,这却并不容易:当我们把一个分类的准确率提高了,这一改动可能会使另一分类的准确率降低。只有我们找到了对所有分类都合适的参数,才能获得良好的分类表现。
想象一个仅有俩参数的神经网络(比如:-0.37和1.14),再想象你站在高岗上向下望,海拔就是分类误差,水平上的两个方向x-y代表这两个参数,任务就是找到最low的那一点——误差最低。
问题在于,我们看不到这边山地的全景,就像深处迷雾之中,只知道当前的位置(初始随机参数)和高度(当前分类误差)。只有这点儿信息,怎样快速找到最low点呢?

随机梯度下降(Stochastic Gradien Descent)
想象你伫立在山头上,脚著谢公屐,身登青云梯。你想以最快速度到达谷底,但是浓雾弥漫,目之所及只有几步的视野,咋整?环视四周,选了一个最陡峭的方向,往那边儿一出溜;再看看四周,找到新的最陡方向,又是一出溜。由此循环往复,不断地滑动——这就是梯度下降法。
梯度下降法就像每10米停一下,然后掏出全套长枪短炮,测量一下周围的坡度(根据全局数据测量梯度);而随机梯度下降法就是大概瞅一眼就找个方向(只用几百个数据点预测坡度)。
在随机梯度下降算法中,我们在误差函数的曲面上,走最陡峭的下坡路(梯度或一阶导数的负数),想找到最低点。我们亦步亦趋,小步快走,步子不要太大是为了防止在一个坑里来回拉锯。
我们设想的场景是3D的,而实际上很多误差空间可能有好几百万个维度。在这样的空间里,我们会有很多的“谷”,所以找到一个好的解并不难,但同时我们还有很多鞍点,让情形更复杂了。
鞍点附近像是一片平原,在这样的误差空间里找到一个解很困难。因为周围几乎没有坡度,过程在鞍点周围会变得极其缓慢,突破这一束缚可能比找到最低点本身还要难。
延伸阅读:Coursera: Neural Networks for Machine Learning: Optimization – How to Make the Learning Go Faster
误差的反向传播(BackPropagation of Errors)
误差的反向传播,或简称反向传播,是在神经网络中找到误差相对权重梯度的方法。梯度表示误差会随着权重如何变化。这里的梯度用于执行梯度下降算法,最终得到一组权重使得网络误差最小。

图2:深度神经网络里任意一层的反向传播
教授反向传播有三种比价好的方式:(1)可视化表示,(2)数学表示,(3)基于规则的表示。本节的延伸阅读用的是数学表示。这里我将用基于规则的表示,因为这不需要太多数学理论,而且容易理解。
假设有个神经网络里有100层,我们可以想象一个前馈过程:一个矩阵(维度:样本数量 x 输入节点数)输入到网络并传播,我们始终有(1)输入节点,(2)权重矩阵(维度:输入节点 x 输出节点),(3)输出节点带有非线性激励函数(维度:样本 x 输出节点)。怎么来想象这些矩阵呢?
输入矩阵:每个输入节点与偶一个输入值,比如像素值(三个输入值 = 图1里的三个像素),乘以样本数量,即图片数。所以对于128张3像素图片,我们的输入矩阵就是128×3。
权重矩阵代表输入和输出节点之间的连接,通向输入节点(像素)的值,经过权重矩阵加权,再“流”向每个输出节点。这个“流”是输入值和每个权重值相乘的结果。输出矩阵就是所有输出节点收到的,来自所有输入节点的累积“流”。
对于每个输入,我们乘以所有权重,再相加给予输出节点,或者更容易的是,直接求输入矩阵和权重矩阵的矩阵相乘。在这个例子里就是128×3的输入矩阵与3×5的权重矩阵相乘。 然后得到输出矩阵128×5。我们将对这一输出矩阵应用非线性激励函数,并将结果作为输入矩阵再传递给下一层。重复这一过程,直到得出误差函数。通过误差函数可以计算我们的预测与正确值之间的差距,这就是正向传播过程。
输入数据的正向传播过程,从第一层到最后一层,基于如下规则:
遇到权重矩阵,进行矩阵乘法,继续传播结果。
遇到激励函数,将现有结果传递给激励函数,并传播函数输出。
将上一层的输出,作为下一层的输入。
遇到误差函数,计算误差,留待反向传播使用。
误差的反向传播过程类似,只是从最后一层到第一层,基于如下规则:
遇到权重矩阵,与其转置相乘,传播结果。
遇到激励函数,逐个元素地乘以该函数(相对前馈输入)的导数。
将前一层的误差当作后一层的输入。
为了计算梯度,我们用反向传播规则2的中间结果,与争先传播规则2的中间结果,进行矩阵乘法。
延伸阅读: Coursera: Neural Networks for Machine Learning: The Backpropagation Learning Procedure
修正线性函数(ReLU)
修正线性函数具有简单的非线性性质:保留正值,将负值变成0:f(x) = max(0, x)。ReLU对所有正值的梯度是1,负值的梯度为0。这意味着在反向传播过程中,负梯度不会用于更新ReLU的输出权重。
然而,因为我们对正值有梯度1,所以训练速度相比其他非线性单元更快。比如logistic sigmoid函数在大绝对值处的梯度很小,以致于学习过程几乎停滞(这一情形与鞍点问题相似)。
除了负梯度不传播(梯度为0)以外,“大正值有大梯度”也是ReLU的优势,无论梯度几何,训练速度都很快。自从这一优势被发现以来,ReLU以及其他有大梯度的激励函数就成为深度网络的首选。
动量/Nesterov’s
加速的梯度
梯度的下降路径呈锯齿状的,不过大致上还是向着最小值的一条直线。如果我们在这个方向上移动再快一点,而减少曲折来回,就能更快地抵达终点。这就是动量思想。
让我们跟踪一个移动中的动量矩阵,也就是梯度加权和,我们把这个矩阵的值加到梯度上。动量矩阵的尺寸始终在控制之中,每次更新(乘以一个动量值:0.7~0.99之间)都要消减。经过一段时间,锯齿将被动量矩阵平滑化:一个方向上的锯齿与其相反方向的锯齿抵消,形成通往局部最小值的直线。最开始,这个大致方向还没有建立起来,动量矩阵需要消减的更猛烈些,否则动量值反而会放大锯齿震荡,是学习过程失稳。因而,动量开始应该保持较小取值(0.5~0.7),之后再迅速放大(0.9~0.999)。
通常先尽形得势梯度更新,再跳到动量方向。但是Nesterov指数,先跳到动量方向,再用梯度更新修正方向,效果更好。这一过程就是“Nesterov加速梯度”,收敛更快。
延伸阅读:Coursera: Neural Networks for Machine Learning: 3. The Momentum Method
均方根传播(Root Mean Square Propagation)
RMSprop跟踪梯度平方的加权移动均值,再求平方根(本质上,就是除以最近梯度的大小,对梯度归一化)。当误差平面进入平原地带,梯度很小的时候,更新使用更大步幅以保证快速收敛(小幅更新:0.00001,加权平均的平方根:0.00005,更新规模:0.2)。另一方面,RMSprop还防止了梯度激增(大更新:100,加权平均的平方根:25,更新规模:4),所以在循环神经网络和LSTM中使用很多,来防止梯度消失和梯度爆炸。
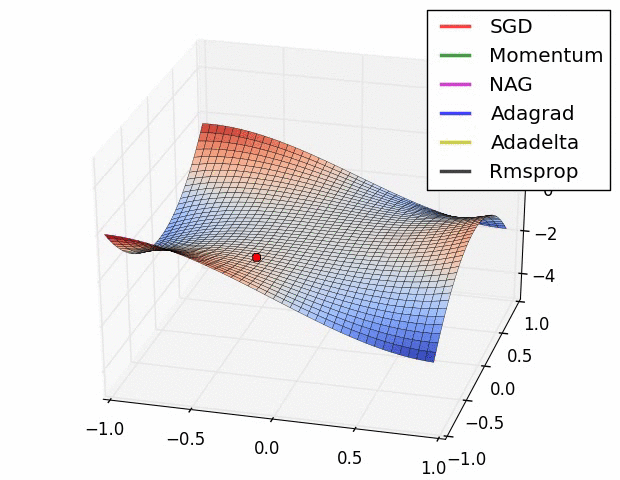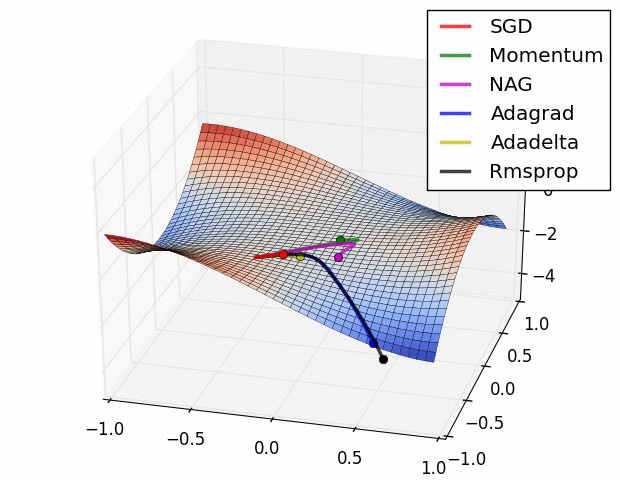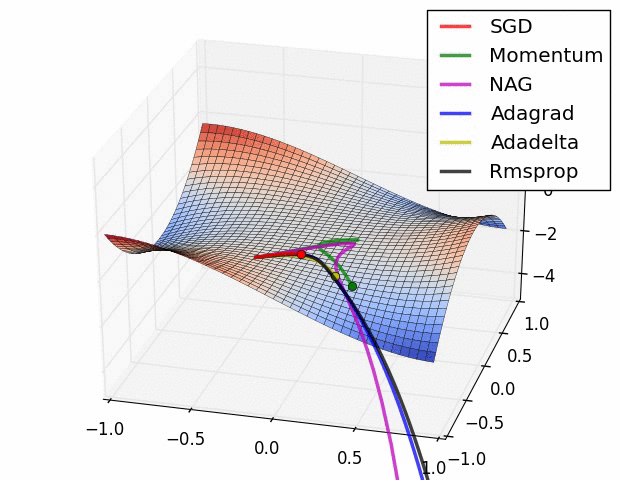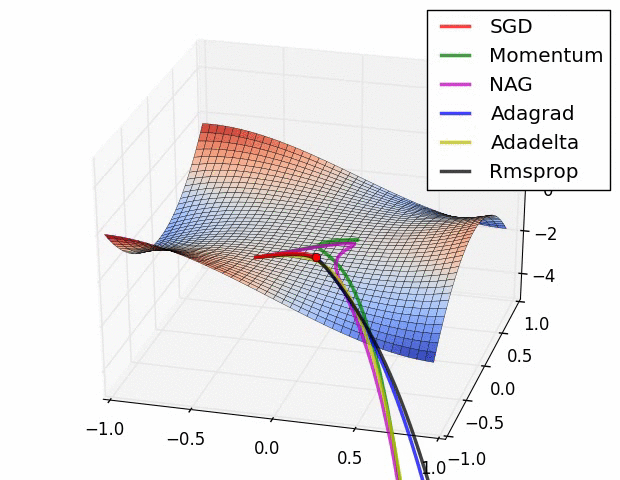
图3:鞍点处加速梯度下降的不同方法。鞍点是优化深度网络中的主要困难。Image by Alec Radford
延伸阅读:Coursera: Neural Networks for Machine Learning for Machine Learning: RMSProp
Additional animations comparing different optimization problems.
Dropout
想象你(卷积网络中的一个单元),正在准备一场考试(分类任务),并且考试期间允许抄袭(其他单元)。那你还会学习吗?答案或许取决于,这个班上是否至少有那么几个人还是学了。
假设你知道班里(神经网络)里有两个学生(单元)久负学霸之名,每门考试(数据集里的每张图片)都会认真复习。所以你就不学了,等着直接抄他们的(从前一层的“精英”单元里复制权重)。
现在突然爆发了一场流感,影响了50%的学生。所以有很大概率,那两名学霸无法参加考试。于是就不能指望他们保你不挂,这一次必须得自己学了(不能只考虑精英单元,而要放眼层中所有单元)。
换言之,Dropout切断了单元之间的信息处理关联,让他们无法依赖于几个“明星”单元,尽管这几个单元看起来很正确(检测出了更重要的特征)。
Dropout使得分类过程更加“民主化”了 ,每个单元都要独立做出计算,以此减少偏差,屏除极端。单元间的的独立带来了很强的正则化和更好的模型泛化能力(集体的智慧)。
L1和L2正则化
L1和L2正则化对网络权重的规模施加了惩罚项,所以高可信度的大输出值不会仅有一个大权重得出,而是需要多个中等规模。尽管很多单元还是得随大流,至少这样可以避免输出值被某一个单元拐得太偏。从概念上讲,L1/L2正则化惩罚单一单元的强意见,而鼓励多个单元的综合意见,以此减少偏差。
L1正则化惩罚的是权重的绝对值,L2惩罚的是权重值平方。这些惩罚项加在误差函数值上,故而权重越大误差越大。结果就是网络被调教地倾向于用小权重解决问题。
很小的权重也会产生挺大的L1惩罚,L1还有一个效果就是,如果存在若干较大权重,其他权重会被设为0。因为非零权重越少,网络可信度越高。
L2惩罚则鼓励很小的非零权重(大权重 -> 大误差)。预测几乎由所有权重共同得出,以此减小偏差(哪个权重也不能一家独大)。
延伸阅读:Coursera: Neural Networks for Machine Learning: 2. Limiting the Size of the Weights