吴恩达机器学习一站式学习系列(8)——神经网络的学习Neural Networks: Learning
代价函数Cost Function
假设神经网络的训练样本有m个,每个包含一组输入x和一组输出信号y,L表示神经网络层数,S_I表示每层的neuron个数(S_l表示输出层神经元个数),S_L代表最后一层中处理单元的个数。
将神经网络的分类定义为两种情况:二类分类和多类分类,
二类分类:S_L=0 , y=0 or 1 表示哪一类;
K类分类:S_L=K , y_i=1表示分到第i类;(k>2)
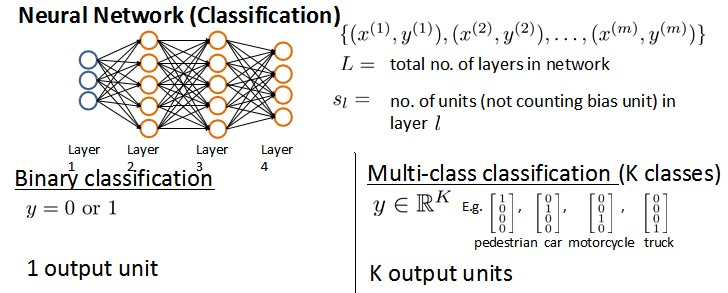
在逻辑回归中,我们只有一个输出变量,又称标量(scalar),也只有一个因变量y,但是在神经网络中,我们可以有很多输出变量,h_θ(x)是一个维度为K的向量,并且训练集中的因变量也是同样维度的一个向量,因此代价函数会比逻辑回归更加复杂一些,为:
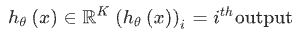
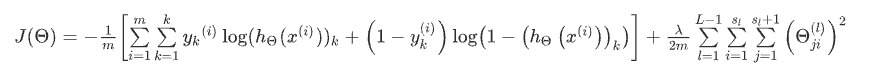
这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出K个预测,基本上我们可以利用循环,对每一行特征都预测K个不同结果,然后在利用循环在K个预测中选择可能性最高的一个,将其与y中的实际数据进行比较。
正则化的那一项只是排除了每一层θ_0后,每一层的 θ 矩阵的和。最里层的循环j循环所有的行(由s_l +1 层的激活单元数决定),循环i则循环所有的列,由该层(s_1层)的激活单元数所决定。即:h_θ(x)与真实值之间的距离为每个样本-每个类输出的加和,对参数进行regularization的bias项处理所有参数的平方和。
反向传播算法Backpropagation Algorithm
反向传播算法(Backpropagation Algorithm)是训练神经网络的关键步骤之一,它通过计算代价函数对于网络参数的梯度,来更新网络参数,以使代价函数的值逐步减小,从而优化网络的性能。
反向传播算法的核心思想是基于梯度下降优化算法,通过不断地调整网络参数,使代价函数逐渐减小,从而提高模型的性能。它是神经网络训练的基石,使网络能够逐渐学习如何正确地进行分类、回归或其他任务。
正向传播(Forward Propagation)和反向传播(Backpropagation)是神经网络训练中的两个关键步骤,它们分别用于计算网络的输出和更新网络的参数。
正向传播(Forward Propagation): 正向传播是指在神经网络中将输入数据从输入层经过各个隐藏层传递到输出层的过程。在正向传播中,每个神经元将前一层的输出(激活值)乘以对应的权重,并将这些加权和输入到该层的激活函数中。这个过程逐层进行,直到输出层产生最终的预测结果。正向传播不涉及梯度计算,只是单纯地通过网络的参数进行计算,从而得到预测结果。
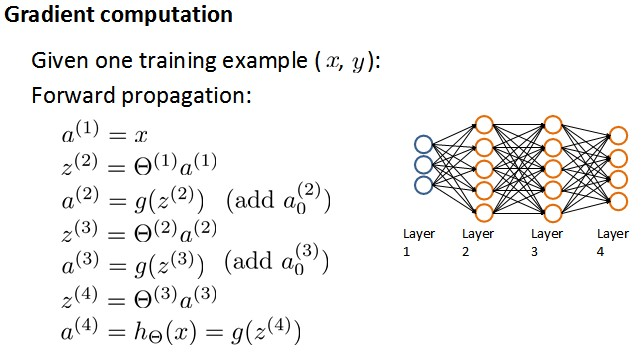
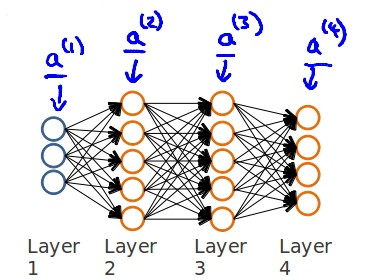
反向传播(Backpropagation): 反向传播是指在神经网络中通过计算代价函数对于网络参数的梯度,来更新网络的参数,以最小化代价函数的值。在反向传播中,首先通过正向传播计算出网络的预测值,然后计算代价函数的值。接着,根据链式法则从输出层开始计算每一层的误差项,然后计算权重和偏置的梯度。这些梯度被用于更新网络参数,使得代价函数减小。反向传播是梯度下降等优化算法的核心,它确保了网络参数朝着使代价函数减小的方向更新。

| 方面 | 正向传播 | 反向传播 |
| 计算过程 | 从输入到输出的前向计算 | 从输出到输入的后向计算 |
| 目标 | 计算网络的输出 | 计算网络参数的梯度 |
| 涉及的计算 | 纯粹的权重和激活函数计算 | 梯度计算和参数更新 |
| 用途 | 得到预测结果 | 优化网络参数 |
| 输入 | 输入特征 | 期望输出和实际输出 |
| 输出 | 预测结果 | 参数梯度 |
| 需要的信息 | 权重、偏置和激活函数 | 权重、偏置、激活函数和误差 |
| 梯度计算 | 不涉及梯度计算 | 使用链式法则计算梯度 |
| 参数更新 | 无 | 使用梯度下降更新参数 |
| 阶段 | 前向计算 | 反向计算 |
| 关键作用 | 计算预测结果 | 计算梯度和更新参数 |
| 算法顺序 | 单向传播 | 反向-前向传播 |
反向传播算法的直观理解Backpropagation Intuition
下面是反向传播算法的基本步骤:
- 前向传播(Forward Propagation):将输入样本通过神经网络进行前向传播,计算每一层的激活值(输出),直至得到最终预测值。同时,保存每一层的中间结果(例如,激活函数的输入和输出)以备后用。
- 计算代价函数(Compute Cost):使用预测值和实际目标值,计算代价函数的值,这个值反映了模型的性能。代价函数可以根据问题的不同而选择,如前面所述的均方误差、交叉熵等。
- 反向传播误差(Backward Propagate Error):从输出层开始,计算每一层的误差项,这是代价函数对于每一层输入的梯度。误差项可以通过链式法则计算得到。对于输出层的误差项,可以根据代价函数的导数直接计算。对于隐藏层,误差项是上一层误差项与权重矩阵的乘积,再乘以激活函数的导数。
- 计算梯度(Compute Gradients):使用误差项计算每一层的权重梯度和偏置梯度。权重梯度是输入的激活值与误差项的乘积,而偏置梯度等于误差项本身。
- 参数更新(Update Parameters):根据计算得到的梯度,使用优化算法(例如梯度下降)来更新网络的权重和偏置。优化算法会根据梯度的方向和大小来更新参数,以使代价函数减小。
- 重复迭代(Iteration):重复执行步骤 1-5,使用不同的训练样本,直到代价函数收敛或达到预设的迭代次数。
反向传播算法可以通过以下步骤来更直观地理解:
- 建立类比:想象你是一个登山者,目标是到达山顶。你所面临的是一个多层山脉,每一层都是神经网络的一层。你的目标是找到一条路径,以便在山脉中找到最低的山谷,这个山谷代表代价函数最小化的位置。
- 下山的步骤:为了下山,你需要感受地势的变化。这就是我们在神经网络中所做的正向传播。你向前走一步一步,观察每一步的高度变化,直到你到达山底,这就是我们得到的预测值。
- 找到下降方向:为了下山,你需要知道每一步应该向哪个方向前进。这就是梯度的作用。在神经网络中,梯度告诉我们应该如何调整参数,以便代价函数减小。
- 反向传播:在山脉中,你无法直接感受到所有方向的高度变化。但是,你可以观察自己在下山过程中的每一步,然后回顾自己的行动,以确定哪些步骤导致了更快的下降。这就是反向传播的概念。我们通过观察每一步的变化(正向传播的结果)并从山底向上回溯,来计算每一步的影响,以确定如何调整参数以最小化代价函数。
- 更新参数:一旦你知道了哪些方向会让你更快地下山,你可以调整你的步伐,以便更有效地接近山谷。在神经网络中,梯度信息告诉我们应该增加或减少每个参数,以便更好地拟合数据。
- 迭代过程:你不会一次就到达山谷,你需要不断地重复这个过程,以便找到最佳路径。在神经网络中,我们也需要多次迭代,每次迭代都会微调参数,逐渐优化模型。
前向传播算法:
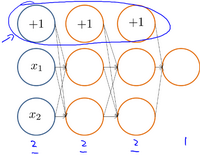

反向传播算法

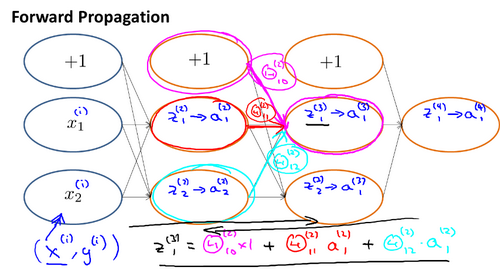
实现注意:展开参数Implementation Note_ Unrolling Parameters
神经网络的参数展开通常是指将网络中所有的权重和偏置连接成一个单一的向量,从而方便进行优化算法(如梯度下降)的计算和更新。这个操作也称为参数平铺(Flattening Parameters)或参数展平(Flattening)。具体来说,对于每一层的权重矩阵和偏置向量,将它们按顺序连接成一个大的向量。
假设一个简单的三层神经网络,其中第一层有2个输入节点,第二层有3个隐藏节点,第三层是输出层有1个输出节点。那么,参数展开过程如下:
- 第一层权重矩阵:2×3 的矩阵,需要展开为 2×3 = 6 个参数。
- 第一层偏置向量:3 个参数。
- 第二层权重矩阵:3×1 的矩阵,需要展开为 3×1 = 3 个参数。
- 第二层偏置向量:1 个参数。
总共有 6 + 3 + 3 + 1 = 13 个参数。这些参数可以按照特定顺序连接成一个参数向量,然后使用这个参数向量进行优化算法的计算和更新。

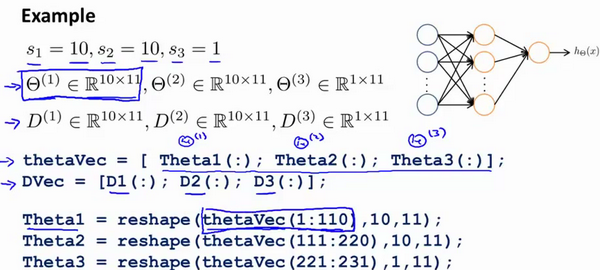

在实际操作中,参数展开对于神经网络的训练和优化是非常有用的,因为它简化了计算和更新的过程,并且可以更有效地管理大规模网络的参数。在大型深度神经网络中,参数数量可能会非常巨大,因此参数展开可以帮助减少管理这些参数所需的复杂性。
梯度检验Gradient Checking
梯度检验(Gradient Checking)是一种用于验证梯度计算是否正确的技术。在训练神经网络时,反向传播算法用于计算参数的梯度,以便更新网络参数。然而,实现正确的反向传播可能会有一些困难,因此梯度检验可以帮助验证你的实现是否正确。
梯度检验的基本思想是使用数值方法近似计算梯度,并将其与反向传播得到的梯度进行比较。如果这两个梯度接近,则可以认为反向传播实现是正确的。
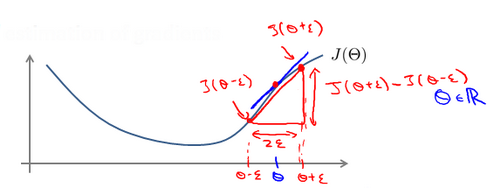
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的θ ,我们计算出在θ-ε处和 θ+ε 的代价值(ε是一个非常小的值,通常选取 0.001),然后求两个代价的平均,用以估计在 θ 处的代价值。
梯度检验的主要目的是在实现反向传播时排除错误。如果梯度检验发现反向传播的梯度与数值梯度之间有明显的差异,那么可能需要仔细检查反向传播的实现并进行修正。然而,值得注意的是,梯度检验是一个相对较慢的过程,通常在调试时使用,而不是在训练过程中每次迭代都执行。
随机初始化Random Initialization
在训练神经网络时,参数的初始值是非常重要的,因为不同的初始值可能会导致不同的收敛性和性能。随机初始化(Random Initialization)是一种常用的参数初始化方法,它的目标是打破对称性,使得每个神经元可以学习不同的特征。
如果所有的参数都被初始化为相同的值,那么在网络的前向传播和反向传播过程中,所有的神经元会被更新成相同的值,从而失去了网络的表达能力。通过随机初始化,每个神经元将会具有不同的初始值,这有助于网络学习到更多不同的特征和模式。
随机初始化可以应用于网络的权重(连接权重)和偏置(biases)。常见的随机初始化方法包括:
- 均匀分布(Uniform Distribution):在一个指定的范围内随机生成参数的初始值,比如从一个均匀分布中随机采样。
- 正态分布(Normal Distribution):使用高斯分布(正态分布)随机生成初始值。这种方法也叫做高斯初始化。
- 稀疏初始化(Sparse Initialization):对于某些网络结构,可以将大多数权重初始化为零,只有一小部分进行随机初始化。
- Xavier / Glorot 初始化:这是一种针对特定激活函数的初始化方法。它根据输入和输出的数量来调整初始值的尺度,以便更好地在前向和反向传播中保持梯度的合理范围。
- He 初始化:类似于Xavier初始化,但适用于使用ReLU(Rectified Linear Unit)等修正线性激活函数的情况。
合适的随机初始化方法取决于网络结构、激活函数等因素。不正确的初始化可能导致训练过程非常缓慢,甚至导致梯度消失或爆炸等问题。因此,选择适当的随机初始化方法对于训练成功的神经网络非常重要。
警告:到目前为止我们都是初始所有参数为0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非0的数,结果也是一样的。
综合起来 Putting It Together
网络结构:第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少个单元。
第一层的单元数即我们训练集的特征数量。最后一层的单元数是我们训练集的结果的类的数量。如果隐藏层数大于1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络:
- 参数的随机初始化
- 利用正向传播方法计算所有的
- 编写计算代价函数 的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法检验这些偏导数
- 使用优化算法来最小化代价函数
The post 吴恩达机器学习一站式学习系列(8)——神经网络的学习Neural Networks: Learning first appeared on PMSOLO.