吴恩达机器学习一站式学习系列(13)— 降维 Dimensionality Reduction
降维(Dimensionality Reduction)是指将高维数据集中的特征维度减少到较低维度的过程。高维数据集通常包含大量特征,而降维的目标是保留尽可能多的信息,同时减少数据的维度,以便更容易可视化、分析和建模。降维技术在数据挖掘、机器学习和数据分析中具有重要作用。
降维的两种主要方法是:
特征选择(Feature Selection):
- 特征选择是通过选择最重要的特征来减少维度。这些特征通常与目标变量或任务的性能关系最大。
- 常见的特征选择方法包括方差阈值、相关系数、互信息、递归特征消除(RFE)等。
- 优点:简单、易于理解,不需要计算新特征。
- 缺点:可能忽略了特征之间的复杂关系。
特征抽取(Feature Extraction):
- 特征抽取通过将原始特征变换为新的特征空间来减少维度。这些新特征通常是原始特征的线性或非线性组合。
- 常见的特征抽取方法包括主成分分析(PCA)、线性判别分析(LDA)、t-SNE、自编码器等。
- 优点:保留了数据的主要信息,可以捕捉特征之间的复杂关系。
- 缺点:计算复杂度较高,可能需要调整参数。
降维的主要优点包括:
- 减少计算复杂度:降维可以大幅减少处理高维数据的计算成本。
- 去除冗余信息:降维可以帮助去除不重要的特征,从而减少噪声和冗余信息的影响。
- 可视化:将数据降维到2D或3D空间可以更容易地可视化数据。
- 增强模型泛化能力:降维可以减少维度灾难问题,有助于提高机器学习模型的泛化能力。
降维的缺点包括:
- 信息损失:降维可能会导致信息损失,尤其是在高度非线性的数据上。
- 参数选择:某些降维方法需要选择参数,这可能需要一些领域知识或交叉验证来确定。
- 难以解释:某些降维方法生成的新特征不易解释,这可能使得解释模型更加困难。
动机一:数据压缩 Motivation I_ Data Compression
降维是什么?作为一种生动的例子,我们收集的数据集,有许多,许多特征。
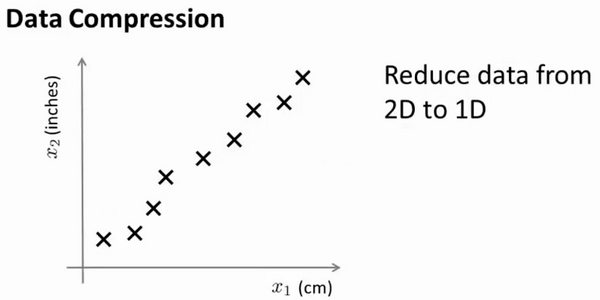
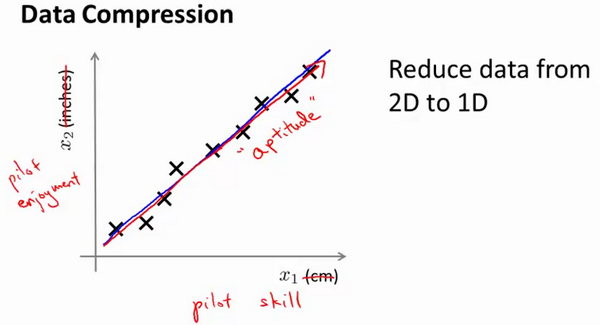
假设我们未知两个的特征:横轴长度用厘米表示;纵轴是用英寸表示同一物体的长度。所以,这是高度冗余表示,也许不是两个分开的特征x1和x2,这两个基本的长度度量,也许我们想要做的是减少数据到一维,只有一个数测量这个长度。
将数据从二维降至一维: 假使我们要采用两种不同的仪器来测量一些东西的尺寸,其中一个仪器测量结果的单位是英寸,另一个仪器测量的结果是厘米,我们希望将测量的结果作为我们机器学习的特征。现在的问题的是,两种仪器对同一个东西测量的结果不完全相等(由于误差、精度等),而将两者都作为特征有些重复,因而,我们希望将这个二维的数据降至一维。
从这件事情我看到的东西发生在工业上的事。如果你有几百个或成千上万的特征,它是它这往往容易失去你需要的特征。有时可能有几个不同的工程团队,也许一个工程队给你二百个特征,第二工程队给你另外三百个的特征,第三工程队给你五百个特征,一千多个特征都在一起,它实际上会变得非常困难,去跟踪你知道的那些特征,你从那些工程队得到的。其实不想有高度冗余的特征一样。
将数据从三维降至二维: 这个例子中我们要将一个三维的特征向量降至一个二维的特征向量。过程是与上面类似的,我们将三维向量投射到一个二维的平面上,强迫使得所有的数据都在同一个平面上,降至二维的特征向量。
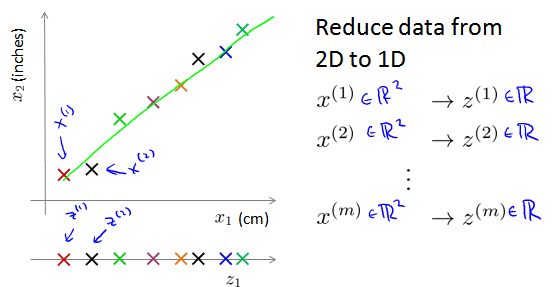
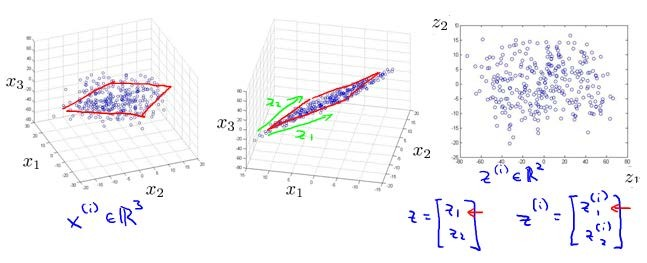
这样的处理过程可以被用于把任何维度的数据降到任何想要的维度,例如将1000维的特征降至100维。
降维在数据压缩中是一种常见的应用。通过将高维数据映射到低维空间,可以实现数据的压缩,从而减少存储空间和计算成本。以下是降维在数据压缩中的一些应用场景和方法:
- 图像压缩:
- 在图像处理中,降维可以用于图像压缩,减少图像的存储空间和传输带宽需求。
- 主成分分析(PCA)和奇异值分解(SVD)是常用于图像压缩的降维方法。
- 音频压缩:
- 在音频处理中,降维可以用于音频信号的压缩,以减小文件大小。
- 基于小波变换的方法和子带编码是音频压缩的常见技术。
- 文本压缩:
- 对于大规模文本数据集,可以使用降维方法来减少特征维度,以节省存储空间和提高文本检索性能。
- 常见的方法包括词嵌入(Word Embeddings)和主题建模。
- 传感器数据压缩:
- 在传感器网络和物联网应用中,可以使用降维来压缩传感器数据,以降低数据传输成本。
- 主成分分析(PCA)和小波变换在传感器数据压缩中常被采用。
- 大规模数据集的存储和分析:
- 对于大规模数据集,降维可以帮助减小数据的规模,以便在计算和存储方面更加高效。
- 例如,通过使用主成分分析(PCA)或t-SNE等方法,可以将高维数据降维到二维或三维空间,以进行可视化和分析。
- 特征工程:
- 在机器学习和数据分析中,降维也可以用于特征工程,以减少特征数量并提高模型训练效率。
- 特征选择和特征抽取方法可以用于在建模前对特征进行压缩。
动机二:数据可视化 Motivation II_ Visualization
在许多及其学习问题中,如果我们能将数据可视化,我们便能寻找到一个更好的解决方案,降维可以帮助我们。
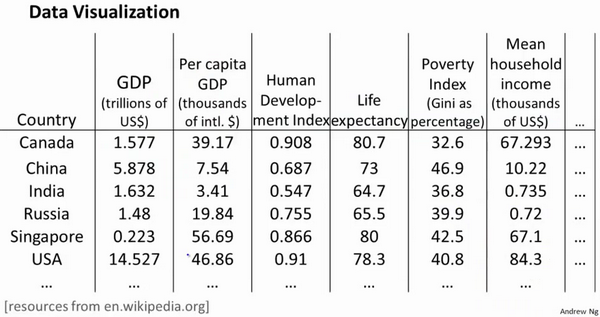
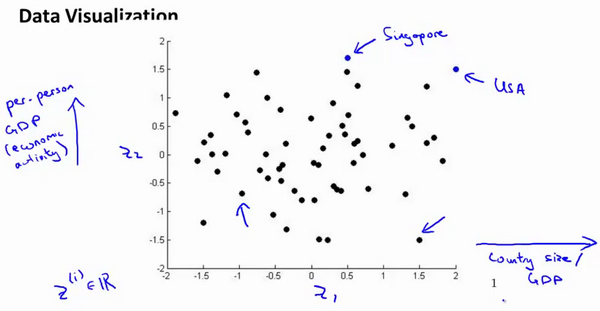
假使我们有有关于许多不同国家的数据,每一个特征向量都有50个特征(如GDP,人均GDP,平均寿命等)。如果要将这个50维的数据可视化是不可能的。使用降维的方法将其降至2维,我们便可以将其可视化了。
这样做的问题在于,降维的算法只负责减少维数,新产生的特征的意义就必须由我们自己去发现了。
降维在数据可视化中有重要的应用,特别是当我们需要将高维数据映射到低维空间以便于可视化时。以下是降维在数据可视化上的一些常见应用场景和方法:
- 高维数据可视化:
- 在高维数据集中,直接可视化数据通常是困难的,因为我们无法在三维或更高维的空间中直观地观察数据。
- 降维技术如主成分分析(PCA)、t-SNE(t-distributed stochastic neighbor embedding)、LLE(局部线性嵌入)等可以将高维数据映射到二维或三维空间,以进行可视化。
- 数据探索和发现:
- 降维可以帮助数据科学家或分析师探索数据并发现潜在的模式和结构。
- 通过在降维后的低维空间中可视化数据,人们可以更容易地观察数据点之间的关系、聚类、异常值等。
- 聚类可视化:
- 在聚类分析中,降维可以帮助可视化不同簇之间的关系和分布。
- 通过降维可视化,可以观察到簇是否分开得足够清晰,或者是否有重叠部分。
- 分类边界可视化:
- 降维可以用于可视化分类模型的决策边界。
- 通过将高维数据映射到二维或三维,可以绘制出分类器在不同特征组合下的决策边界。
- 时间序列可视化:
- 在时间序列数据中,降维可以用于将多维的时间序列数据可视化为更简单的形式。
- 这有助于分析趋势、周期性和异常值。
- 特征重要性可视化:
- 在机器学习中,降维可以帮助可视化特征的重要性。
- 可以通过查看主成分的贡献度或特征在降维空间中的权重来了解哪些特征对于数据变化的解释最重要。
- 多模态数据融合:
- 当数据集包含多个不同类型的特征时,降维可以帮助将多模态数据融合到一个可视化空间中。
- 这有助于分析多模态数据之间的关联性和交互效应。
主成分分析问题 Principal Component Analysis Problem Formulation
主成分分析(PCA)是最常见的降维算法。在PCA中,找到一个方向向量(Vector direction),当我们把所有的数据都投射到该向量上时,希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量,而投射误差是从特征向量向该方向向量作垂线的长度。
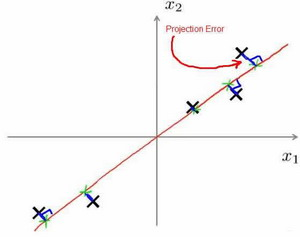
下面给出主成分分析问题的描述:
问题是要将n维数据降至k维,目标是找到向量使得总的投射误差最小。
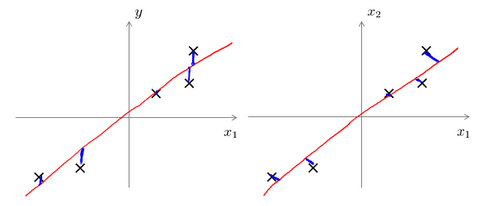
主成分分析与线性回归是两种不同的算法。主成分分析最小化的是投射误差(Projected Error),而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果,而主成分分析不作任何预测。
PCA将n个特征降维到k个,可以用来进行数据压缩,如果100维的向量最后可以用10维来表示,那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA 要保证降维后,还要保证数据的特性损失最小。
PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
PCA技术的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
PCA广泛应用于数据预处理、可视化、特征工程和噪声去除等领域。
以下是PCA的主要步骤和关键概念:
- 标准化数据:
- 首先,对原始数据进行标准化,确保所有特征具有相同的尺度。这通常包括将数据均值中心化并进行标准差缩放。
- 计算协方差矩阵:
- PCA的核心思想是通过计算数据的协方差矩阵来找到数据的主要方向。
- 协方差矩阵的元素表示不同特征之间的关系强度。正值表示正相关,负值表示负相关,而零表示无关。
- 特征值分解:
- 对协方差矩阵进行特征值分解,以找到主成分(特征向量)和它们对应的特征值。
- 特征向量代表主成分的方向,而特征值表示数据在该方向上的方差。
- 选择主成分:
- 根据特征值的大小,选择要保留的主成分。通常,特征值较大的主成分包含了更多的数据方差,因此选择前几个主成分即可保留大部分数据信息。
- 投影数据:
- 将原始数据投影到所选的主成分上,得到降维后的数据集。
- 新的特征向量是主成分,它们是原始特征的线性组合。
- 解释方差:
- 通过特征值的比例,可以解释降维后数据中保留的总方差。通常,可以绘制解释方差的累积图来帮助确定要保留的主成分数量。
PCA的优点和应用包括:
- 降维:通过去除冗余信息,减小了数据维度。
- 噪声去除:主成分通常对噪声不敏感,有助于去除数据中的噪声。
- 可视化:降维后的数据可以更容易地可视化。
- 特征工程:PCA可用于特征选择和特征抽取。
- 压缩:可以用于数据压缩和减小存储需求。
需要注意的是,PCA是一种线性方法,可能不适用于非线性数据。在某些情况下,非线性降维方法如t-SNE可能更合适。此外,在选择要保留的主成分数量时,通常需要进行实验和交叉验证以获得最佳性能。
主成分分析算法 Principal Component Analysis Algorithm

选择主成分的数量 Choosing The Number Of Principal Components

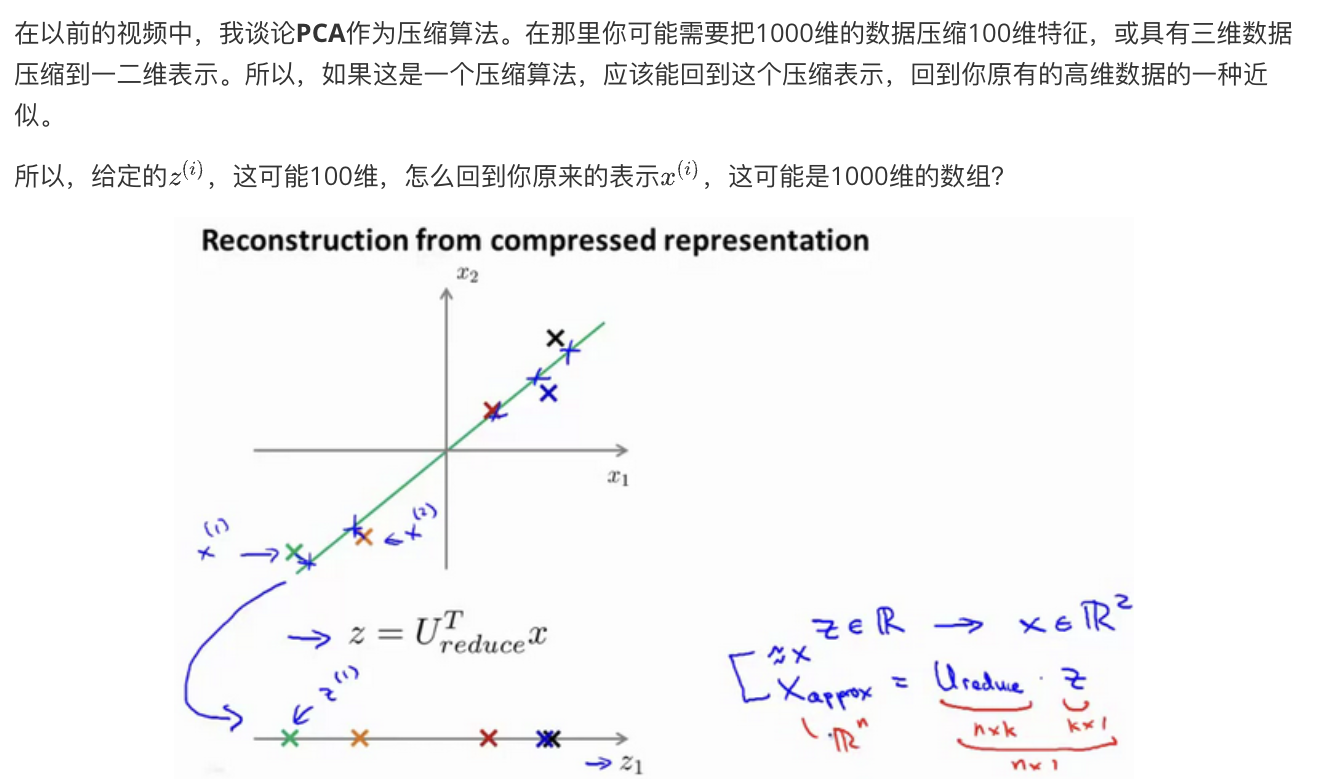
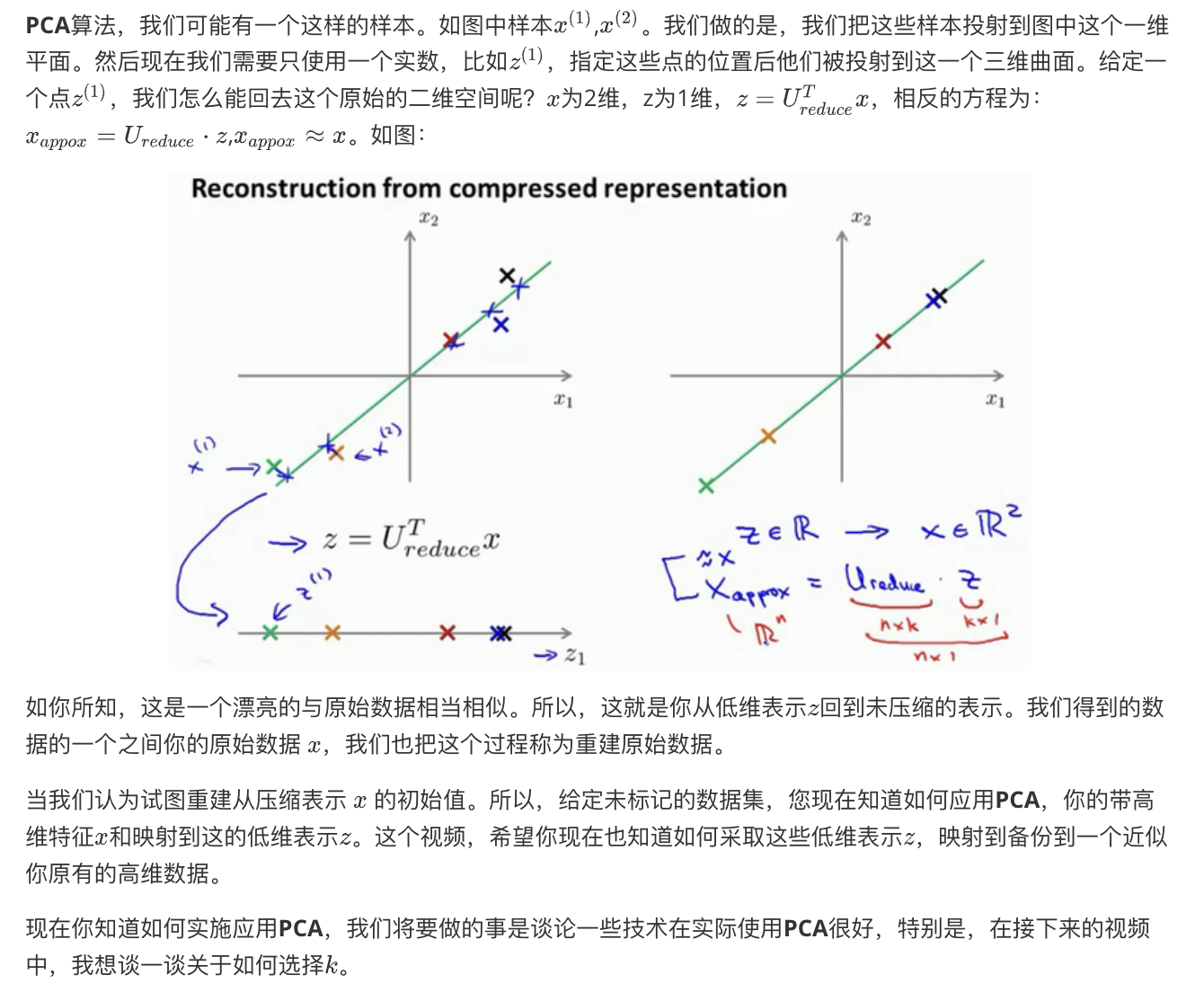
重建的压缩表示 Reconstruction from Compressed Representation
主成分分析法的应用建议 Advice for Applying PCA
假使我们正在针对一张 100×100像素的图片进行某个计算机视觉的机器学习,即总共有10000 个特征。
- 第一步是运用主要成分分析将数据压缩至1000个特征
- 然后对训练集运行学习算法
- 在预测时,采用之前学习而来的向量U将输入的特征转换成特征向量,然后再进行预测
注:如果我们有交叉验证集合测试集,也采用对训练集学习而来的向量U。
错误的主要成分分析情况:一个常见错误使用主要成分分析的情况是,将其用于减少过拟合(减少了特征的数量)。这样做非常不好,不如尝试正则化处理。原因在于主要成分分析只是近似地丢弃掉一些特征,它并不考虑任何与结果变量有关的信息,因此可能会丢失非常重要的特征。然而当我们进行正则化处理时,会考虑到结果变量,不会丢掉重要的数据。
另一个常见的错误是,默认地将主要成分分析作为学习过程中的一部分,这虽然很多时候有效果,最好还是从所有原始特征开始,只在有必要的时候(算法运行太慢或者占用太多内存)才考虑采用主要成分分析。
The post 吴恩达机器学习一站式学习系列(13)— 降维 Dimensionality Reduction first appeared on PMSOLO.