吴恩达机器学习一站式学习系列(12)— 聚类 Clustering
无监督学习:简介 Unsupervised Learning_ Introduction
无监督学习(Unsupervised Learning)是机器学习的一种范式,与监督学习不同,它在训练过程中不使用标签或输出目标。无监督学习的主要任务是从数据中发现隐藏的结构、模式或规律,以便对数据进行聚类、降维、生成等操作。这种学习范式适用于许多现实世界的问题,其中没有事先标记的数据。
以下是无监督学习的一些关键概念和要点:
- 聚类(Clustering):聚类是无监督学习中的一项任务,其目标是将数据分成若干组,每组内的数据点相似度较高,而不同组之间的相似度较低。K均值聚类和层次聚类是常见的聚类算法。
- 降维(Dimensionality Reduction):降维是指减少数据集的特征维度,同时保留尽可能多的信息。降维技术有助于可视化数据和减少计算复杂性。主成分分析(PCA)和 t-SNE 是常用的降维方法。
- 生成模型(Generative Models):生成模型试图学习数据的概率分布,然后可以生成与原始数据类似的新样本。常见的生成模型包括高斯混合模型(GMM)和变分自编码器(VAE)等。
- 关联规则挖掘(Association Rule Mining):关联规则挖掘是一种发现数据中项之间关联关系的方法,常用于市场篮子分析和推荐系统。
- 异常检测(Anomaly Detection):异常检测的目标是识别数据中的异常或离群值,这些值与大多数数据点不同。异常检测在金融欺诈检测和设备故障检测等领域中有广泛应用。
- 无监督学习的应用:无监督学习在许多领域中都有应用,包括自然语言处理、图像处理、生物信息学、推荐系统等。例如,无监督学习可以用于聚类文本文档、降维图像数据、生成艺术作品等。
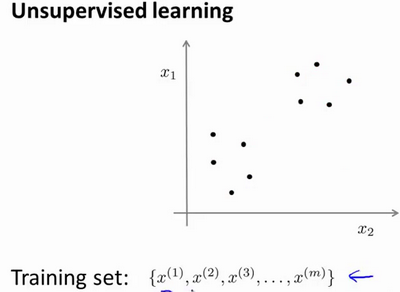
有一系列点,却没有标签,也没有对应的y值。
在非监督学习中,将一系列无标签的训练数据,输入到一个算法中,然后让算法找到这个数据的内在结构。
期间,需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集(称为簇),一个能够找到簇的算法,就被称为聚类算法。
聚类算法一般用来做什么呢?
- 市场分类
- 社交分析和分类
- 文本聚类、主题建模
- 图像分割
- 异常检测
- ……
K-均值算法 K-Means Algorithm
K-均值(K-Means)算法是一种聚类算法,用于将数据点分成 K 个不同的簇或群组。每个簇内的数据点相似度较高,而不同簇之间的数据点相似度较低。K-均值算法是一种迭代的、无监督学习的方法,通常用于数据分析、图像压缩、特征工程等应用。
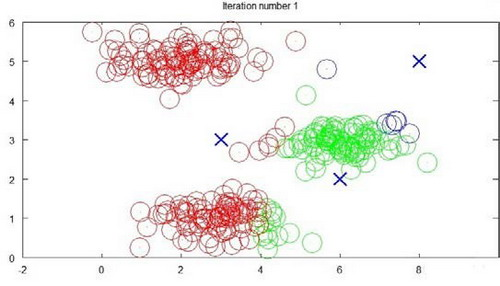
迭代1次
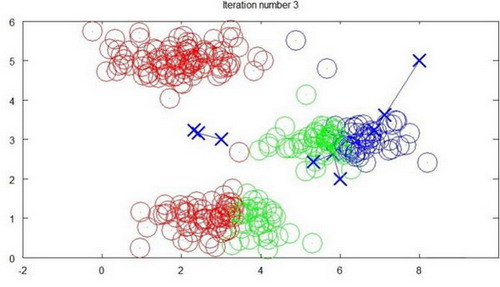
迭代3次
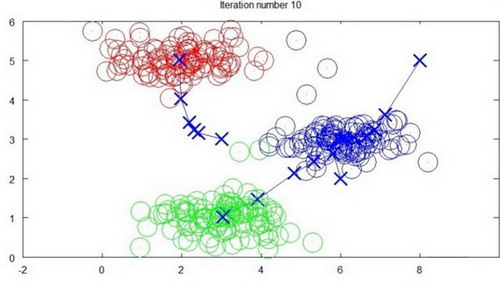
迭代10次
主要步骤:
- 选择 K 值:首先需要选择要划分的簇的数量 K。这可以是根据问题的背景知识或使用不同的 K 值进行试验来确定的。
- 初始化簇中心:从数据集中随机选择 K 个数据点作为初始簇中心。这些中心点将用于定义簇;即聚类中心(cluster centroids)
- 分配数据点:对于每个数据点,计算其与每个簇中心的距离,并将数据点分配到最近的簇中心所代表的簇。
- 更新簇中心:对于每个簇,计算其所有数据点的平均值,将该平均值作为新的簇中心。
- 重复步骤 3 和 4:重复执行步骤 3 和 4,直到簇中心不再发生显著变化,或达到预定的迭代次数。
- 输出结果:K-均值算法的输出是 K 个簇,每个簇包含一组相似的数据点,以及每个簇的中心点。
K-均值算法的特点和注意事项:
- K-均值算法的结果可能会受到初始簇中心的影响,因此可以多次运行算法并选择最好的结果。
- 算法的收敛性不能保证,因此可能陷入局部最小值。这也是为什么多次运行算法的原因。
- K-均值假定每个簇的数据点都服从高斯分布,因此对于非球形簇或不同尺寸的簇效果可能不佳。
- K-均值对异常值敏感,异常值可能会影响簇中心的位置和结果。
- 选择正确的 K 值通常需要一些领域知识或启发式方法,例如肘部法则(Elbow Method)。
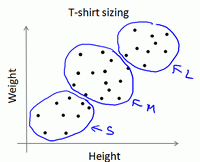
K-均值算法也可以很便利地用于将数据分为许多不同组,即使在没有非常明显区分的组群的情况下也可以。数据集包含身高和体重两项特征构成的,利用K-均值算法将数据分为三类,用于帮助确定将要生产的T-恤衫的三种尺寸。
优化目标 Optimization Objective
K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,因此 K-均值的代价函数(又称畸变函数Distortion function)为:

随机初始化 Random Initialization
运行K-均值算法的之前,首先要随机初始化所有的聚类中心点,下面介绍怎样做:
- 我们应该选择K<m,即聚类中心点的个数要小于所有训练集实例的数量
- 随机选择K个训练实例,然后令K个聚类中心分别与这个K训练实例相等
K-均值的一个问题在于,它有可能会停留在一个局部最小值处,而这取决于初始化的情况。
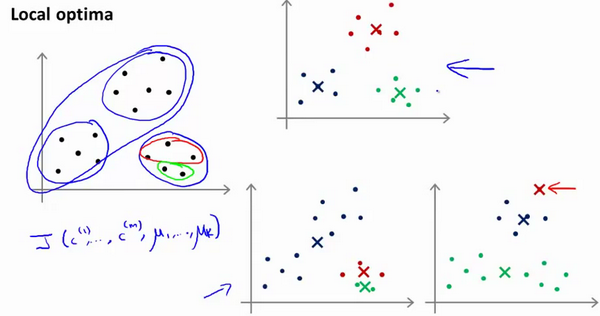
为了解决这个问题,我们通常需要多次运行K-均值算法,每一次都重新进行随机初始化,最后再比较多次运行K-均值的结果,选择代价函数最小的结果。这种方法在K较小的时候(2–10)还是可行的,但是如果K较大,这么做也可能不会有明显地改善。
选择聚类数 Choosing the Number of Clusters
没有所谓最好的选择聚类数的方法,通常是需要根据不同的问题,人工进行选择的。选择的时候思考算法聚类的动机是什么,然后选择能最好服务于该目的标聚类数。
当人们在讨论,选择聚类数目的方法时,有一个可能会谈及的方法叫作“肘部法则”。关于“肘部法则”,我们所需要做的是改变K值,也就是聚类类别数目的总数。我们用一个聚类来运行K均值聚类方法。这就意味着,所有的数据都会分到一个聚类里,然后计算成本函数或者计算畸变函数J。K代表聚类数字。
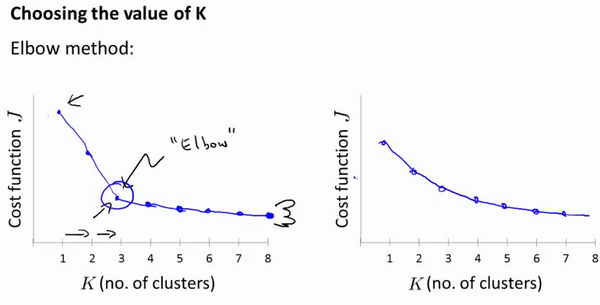
肘部法则(Elbow Method)是一种常用于确定K-均值聚类中最佳簇数量K的启发式方法。该方法基于簇内平方和(Inertia)与簇数量K之间的关系,帮助选择合适的K值,即聚类的数量。
肘部法则的步骤如下:
- 从K=1开始,逐渐增加K的值。对于每个K值,都运行K-均值算法,计算簇内平方和(Inertia)。
- 绘制K值与对应的簇内平方和(Inertia)之间的关系曲线。
- 在曲线上寻找一个“肘部”点,这个点通常是一个拐点,之后簇内平方和的下降幅度开始减小。这个点的K值通常被认为是最佳的K值。
肘部法则的名称来源于图像上曲线的形状,有点像手臂的肘部。通常,肘部点对应的K值表示了数据集中的自然聚类数量。然而,肘部法则并不总是能够清晰地找到肘部点,因此在某些情况下,需要谨慎解释结果。
需要注意的是,肘部法则是一种启发式方法,对于某些数据集和问题,可能没有明显的肘部点,或者有多个潜在的肘部点。因此,在选择K值时,除了肘部法则外,还可以考虑其他方法,如轮廓系数、DBSCAN密度聚类等,以更全面地评估聚类的性能。最终的K值选择应该结合领域知识和实际应用需求。
聚类相关资料
相似度/距离计算方法
相似度和距离计算方法在数据分析、机器学习和聚类等领域中非常重要,它们用于度量数据点之间的相似性或差异。不同的应用和问题可能需要选择不同的相似度/距离度量方法,以下是一些常见的计算方法:

聚类的衡量指标
在聚类分析中,有许多不同的衡量指标可用于评估聚类质量和性能。这些指标可以帮助您了解聚类结果的好坏,并选择合适的聚类算法和参数。以下是一些常见的聚类衡量指标:

The post 吴恩达机器学习一站式学习系列(12)— 聚类 Clustering first appeared on PMSOLO.