OpenCASCADE 曲线求交
OpenCASCADE 曲线求交
1 Introduction
OpenCASCADE中提供了二维几何曲线的求交类Geom2dAPI_InterCurveCurve,对应到三维几何只提供了GeomAPI_IntCS, GeomAPI_IntSS,没有提供几何的GeomAPI_IntCC求交类。这些几何求交一般使用的是数值算法,即解方程。对于两条几何曲线P(u1), Q(u2),求交就是解P(u1) - Q(u2) = 0这个方程。为什么对于三维几何曲线没有提供数值算法?
对于拓朴边提供了求交算法IntTools_EdgeEdge,这个类是使用类似于曲面求交的离散网格法,使用了离散包围盒法。

基于包围合盒的算法是个递归算法,算法思路:
- 1) 检查两条边在参数范围内的包围盒,若空间干涉,则进行下一步;否则退出本次判断;
- 2) 找出两条边包围盒的公共部分对应的参数,若没找到,则退出本次判断;
- 3) 并将第一条边在参数范围内分割成2或3部分,执行第一步;
- 4) 退出条件:没有相交或找到相交的参数值;
第一次是分别分成2部分:
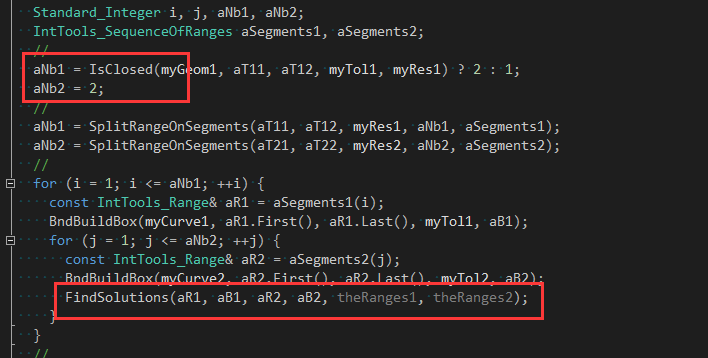
在递归函数FindSolutions()中,只去对第一条边进行参数分割成3部分:
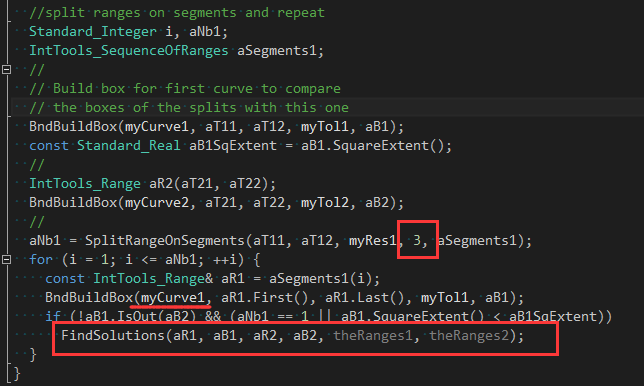
2 辅助函数
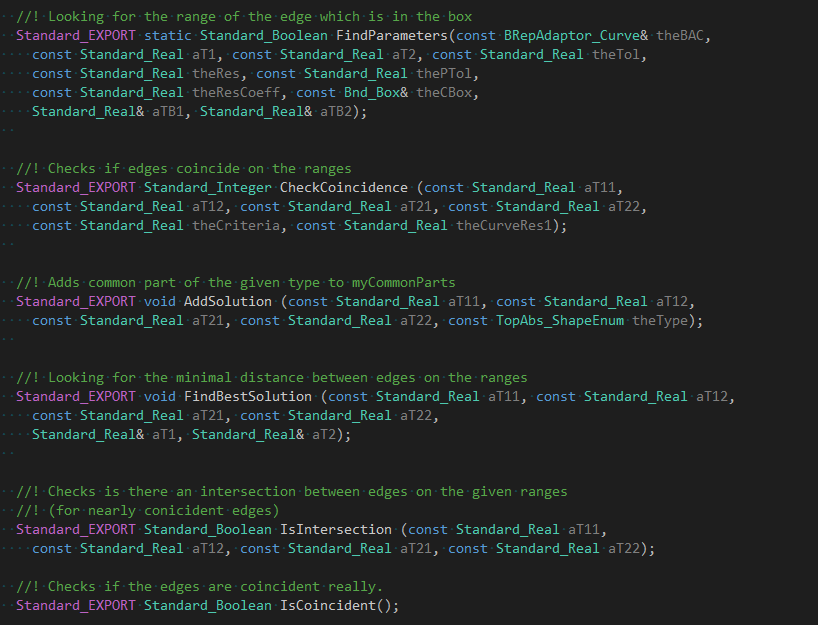
第一个辅助函数是FindParameters(),用来更新第二条边在第一条边的的包围盒中的参数范围,使用这个参数范围更新包围盒。
第二个辅助函数是CheckCoincidence(),用来检测两段边是否重合。第一步是快速计算,对边采样10个点,若通过初步粗检测,后面再深入计算。这些算法都不太高效。
第三个辅助函数是IsIntersection()用来判断两边条在参数范围内是否相交。
3 测试
将两条边求交过程中的包围盒显示出来,方便查看理解算法。先测试两个圆之间的相交:
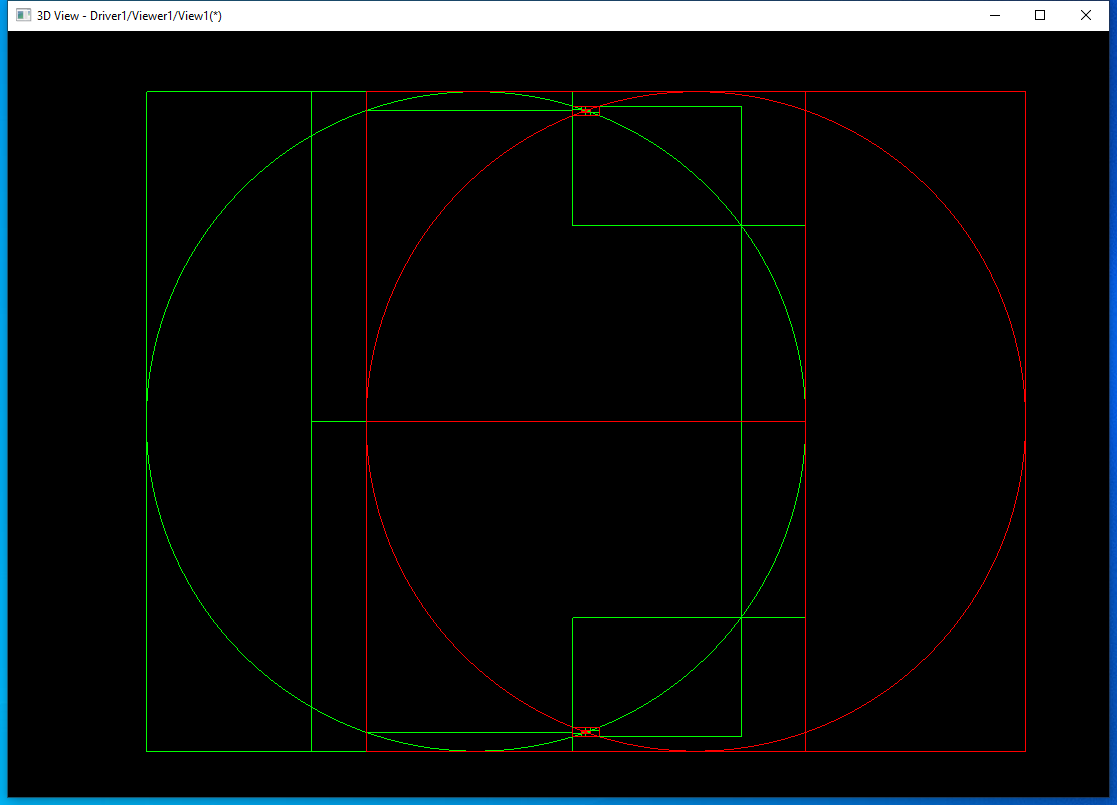
其中第一条边是绿色的圆,求交过程中的包围盒也用绿色表示;第二条边是红色的圆,求交过程中的包围盒也用红色表示。因为圆是闭合的,第一次都分割成2部分。将上面交点处理放大:
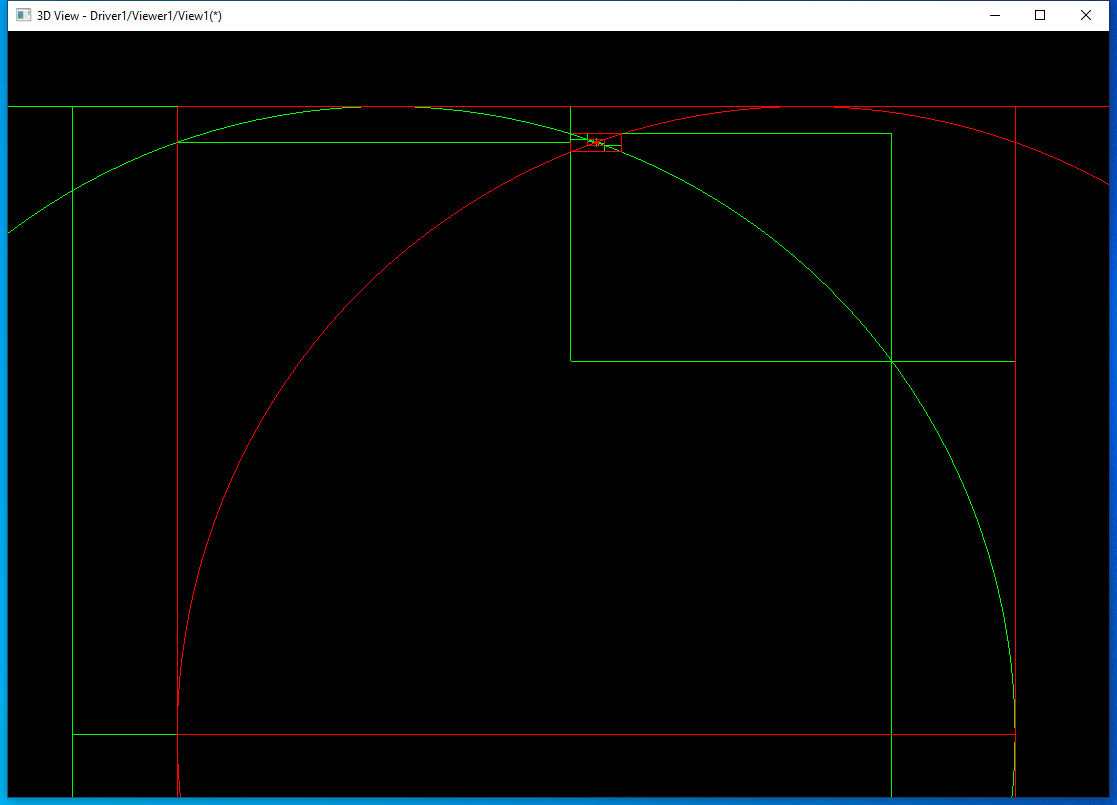
后面都是将第一条边分割成3部分,然后分别用这3部分的包围盒去找与第二条边相交的参数范围,再更新第二条边的包围盒。继续放大上面交点处:
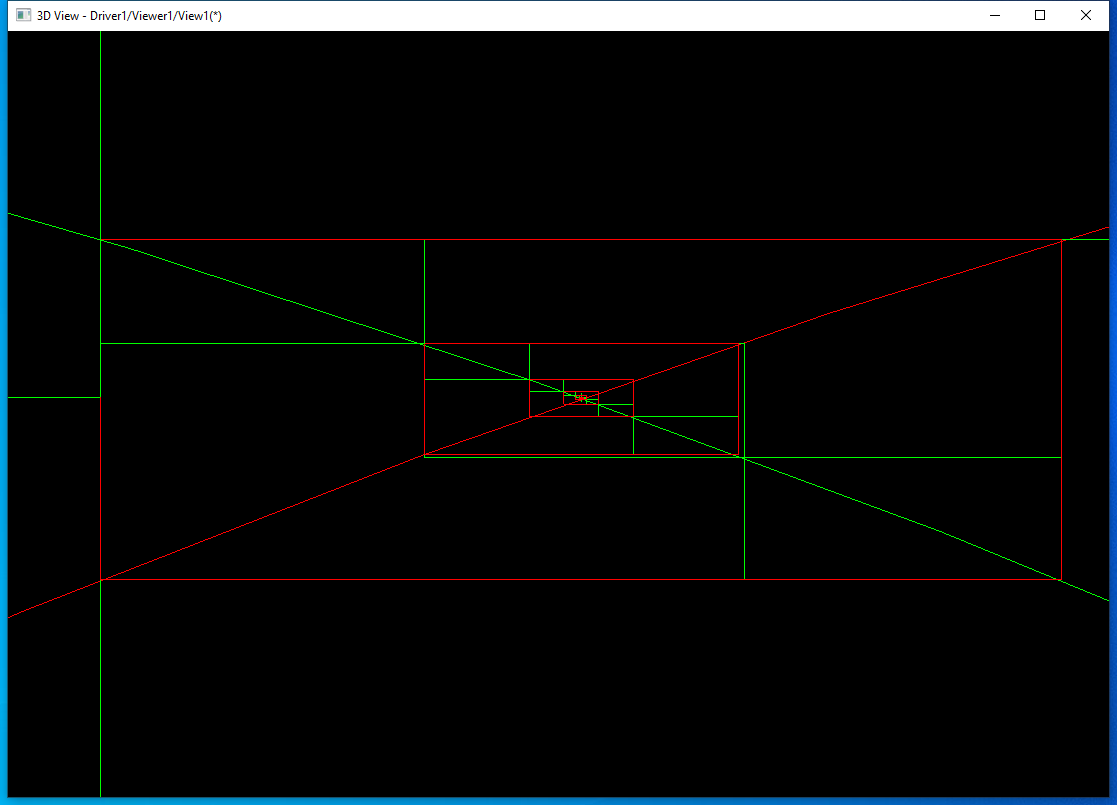
发现对于两个圆的求交,执行了100次,效率不高。又用两个B样条曲线求交来测试:
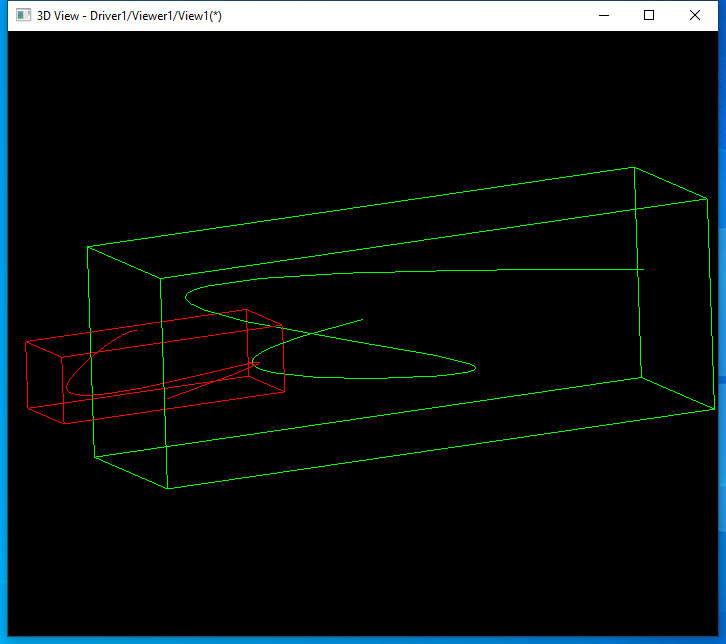
发现对于B样条曲线求交速度较快。
4 Conclusion
曲线求交需要考虑重合部分,opencascae中没有使用数值算法来计算,而是采用基于包围盒的算法来处理。这种算法一般情况下可以快速找到求交解,有时递归较深,对于基本曲线可以像曲面求交一样分类处理以提高性能。opencascade中对于三维曲线求交算法性能还有优化空间。