前言

有一颗二叉搜索树，在不创建任何新节点的条件下，如何将它转换成一个排序的双向链表？本文就跟大家分享下这个算法，欢迎各位感兴趣的开发者阅读本文。

思路分析

在二叉树中，每个节点都有两个指向子节点的指针。在双向链表中，每个节点也有两个指针，分别指向前一个节点和后一个节点。这两种节点的结构很相似，二叉搜索树是一种排序的数据结构，它的左子节点的值总是小于父节点的值，右子节点的值总是大于父节点的值。

那么，我们在将二叉搜索树转换为排序双向链表时：

• 原先指向左子节点的指针，调整为链表中指向前一个节点的指针。
• 原先指向右子节点的指针，调整为链表中指向后一个节点的指针。

如何转换

接下来，我们考虑下如何进行转换。由于转换后的链表是排好序的，我们可以中序遍历树中的每个节点，因为我们在文章实现二叉搜索树-中序遍历中，总结出了它的特点是按照从小到大的顺序访问每个节点。

我们用一个具体的例子来做进一步的分析，当我们执行中序遍历到根节点的时候，就可以把树看成3部分（如下图所示）：

• 值为10的节点
• 根节点值为6的左子树
• 根节点值为14的右子树

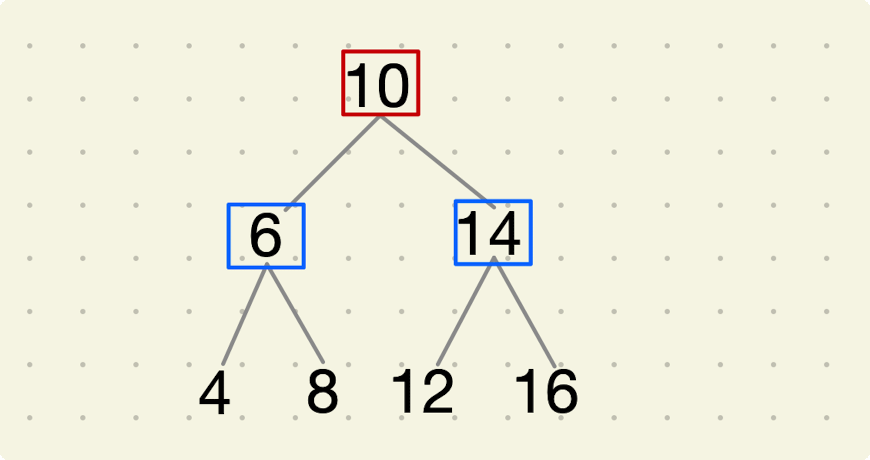
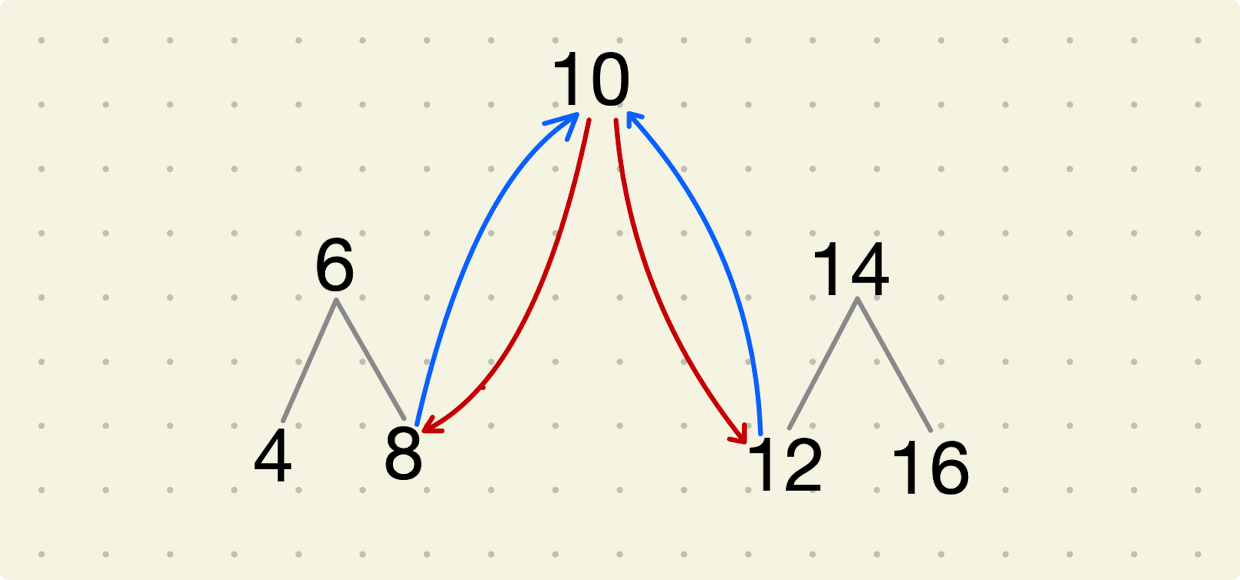
根据排序链表的定义，值为10的节点将和它的左子树中的最大节点（值为8的节点）链接起来，同时它还将和右子树中最小的节点（值为12的节点）链接起来，如下图所示，将其拆成了根节点、左、右子树，我们把左子树与右子树都转换成双向链表之后再和根节点链接起来，整颗二叉搜索树也就转成了排序双向链表。

总结思路

按照中序遍历的顺序，当我们遍历转换到根节点（值为10的节点）时，它的左子树已经转换成一个排序的链表了，并且处在链表中的最后一个节点时当前值最大的节点。我们把值为8的节点和根节点链接起来，此时链表中的最后一个节点就是10了。接着我们去遍历转换右子树，并把根节点和右子树中最小的节点链接起来。

分析到这里，相信大家已经看出了左、右子树节点转换的过程跟遍历的过程是一样的，因此我们可以用递归来解决问题。

• 将左子树构造成双链表，并返回头节点
• 定位至左子树双链表最后一个节点
• 如果左子树链表不为空的话，将当前根节点追加到左子树链表
• 将右子树构造成双链表，并返回头节点
• 如果右子树链表不为空的话，将该链表追加到root节点之后
• 根据左子树链表是否为空确定返回的节点

实现代码

思路捋清之后，接下来我们看下代码的实现。

export function treeToLinkedList(  root: BinaryTreeNode | null | undefined): BinaryTreeNode | null {  if (root == null) return null;  if (root.left == null && root.right == null) return root;  // 将左子树构造成双链表，返回链表的头节点  const leftTree = treeToLinkedList(root.left);  // 遍历左子树双链表，找到它右子树的最后一个节点  let pNode = leftTree;  while (pNode != null && pNode.right != null) {    pNode = pNode.right;  }  // 最后一个节点存在，则将两个节点相互连接起来  if (pNode) {    // 将其右子树与根节点连接    pNode.right = root;    // 将根节点的左子树与其连接    root.left = pNode;  }  // 将右子树构造成双链表，返回链表的头节点  const rightTree = treeToLinkedList(root.right);  // 右子树链表不为空，则将该链表追加到root节点之后  if (rightTree != null) {    rightTree.left = root;    root.right = rightTree;  }  return leftTree != null ? leftTree : root;}

测试用例

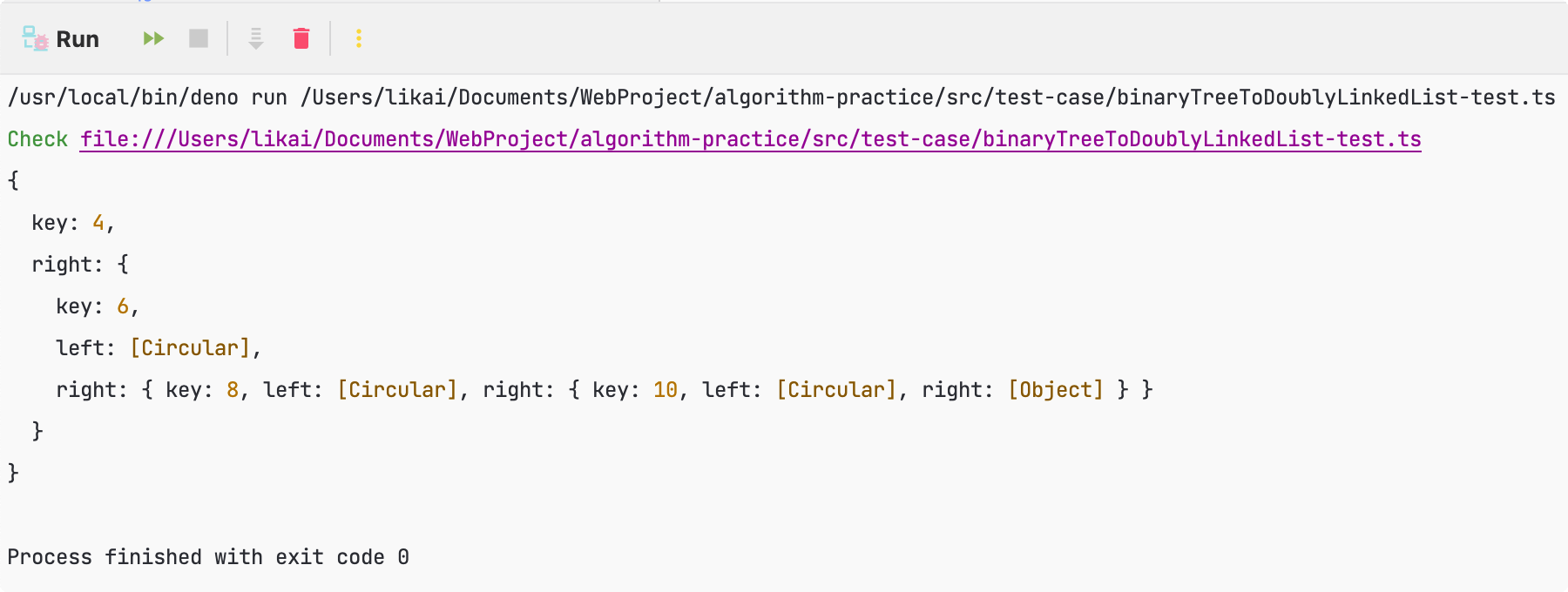
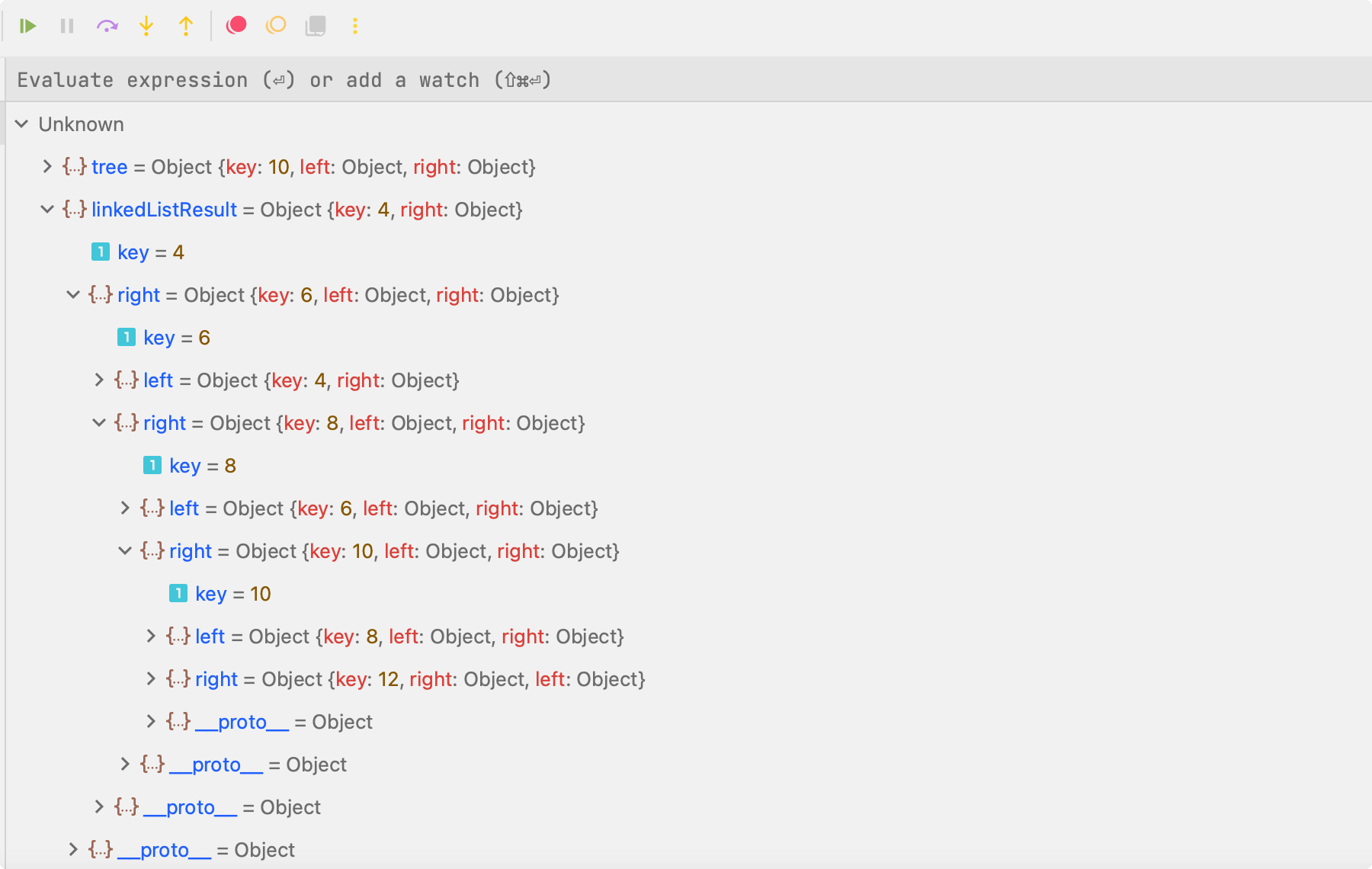
我们用文章中所列举的例子来校验下上述代码能否正确解决问题。

const tree: BinaryTreeNode = {  key: 10,  left: {    key: 6,    left: {      key: 4    },    right: {      key: 8    }  },  right: {    key: 14,    left: {      key: 12    },    right: {      key: 16    }  }};const linkedListResult = treeToLinkedList(tree);console.log(linkedListResult);

执行结果如下所示，正确的将树左右指针所指向的节点进行了更改。

示例代码

本文用到的代码完整版请移步：

• BinaryTreeToDoublyLinkedList.ts
• binaryTreeToDoublyLinkedList-test.ts

写在最后

至此，文章就分享完毕了。

我是神奇的程序员，一位前端开发工程师。

如果你对我感兴趣，请移步我的个人网站，进一步了解。

• 文中如有错误，欢迎在评论区指正，如果这篇文章帮到了你，欢迎点赞和关注😊
• 本文首发于神奇的程序员公众号，未经许可禁止转载💌