前言

有一个整数数组，如何判断该数组是不是某个二叉树的后序遍历结果？本文就跟大家分享下这个算法，欢迎各位感兴趣的开发者阅读本文。

思路分析

我们通过一个例子来分析这个问题，如下所示为一颗二叉树。

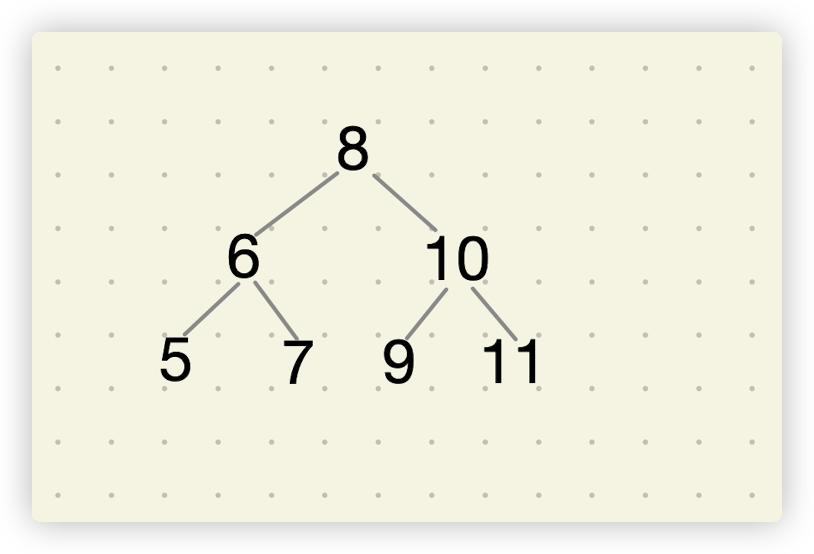
通过之前文章的学习（二叉树的后续遍历），我们可以很快看出这颗树的后续遍历序列为: [5, 7, 6, 9, 11, 10, 8]，通过观察后我们发现最后一个数字为二叉树的根节点，数组中前面的数字可以分为两部分：

• 第一部分是左子树节点的值，它们都比根节点的值小
• 第二部分是右子树节点的值，它们都比根节点的值大

在上面的后续遍历结果数组中，前3个数字5、7、6都比根节点8小，是它的左子树节点；后3个数字9、11、10都比根节点8大，是它的右子树节点。

那么，我们就可以用同样的方法来确定数组每一部分对应的子树的结构。

• 数组5, 7, 6，最后一个数字6是左子树的根节点的值。数字5比6小，是6的左子节点，7则是它的右子节点
• 数组9, 11, 10，最后一个数字10是左子树的根节点的值。数字9比10小，是10的左子节点，11则是它的右子节点

实现思路

通过上面的分析，我们便可以总结出实现思路了。

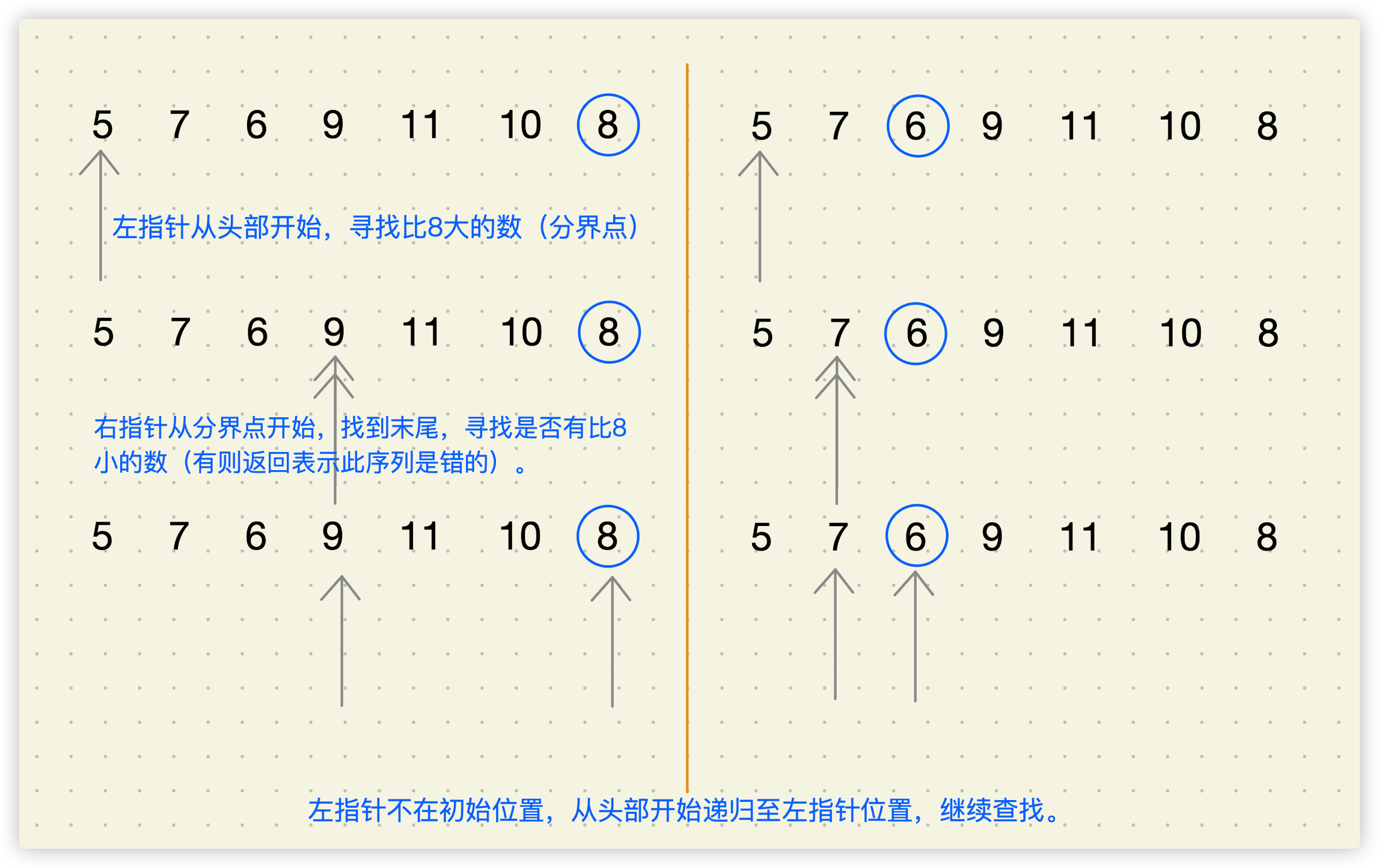
• 最后一项一定是根节点，从根节点前面的值中寻找左、右子树的分界点
• 定义指针leftIndex，前半部分一定是它的左子树，每个节点的值都比根节点小
  • leftIndex默认从0开始，逐渐递增，寻找比根节点大的值，便是它们的分界点
• 定义指针rightIndex，后半部分一定是它的右子树，每个节点的值都比根节点大。
  • rightIndex从分界点开始找（默认从leftIndex位置开始），如果有比根节点小的值，那么这个序列一定不属于二叉树的后序遍历序列
• 如果leftIndex指针离开了起始位置（0），证明它的左子节点还没找完，需要重复执行上述过程继续查找（递归寻找到数组的leftIndex位置）
• 如果leftIndex指针没有到达数组末尾，证明它的右子节点还没找完，需要重复执行上述过程继续查找（从leftIndex+1位置开始递归）
• 返回左、右子树的递归校验结果（两者都为true则表示这个序列为二叉树的后续遍历序列）

实现代码

捋清楚思路后，我们便可以顺利的写出代码了。

  verifySequenceOfBST(sequence: Array<number>, length: number): boolean {    if (sequence == null || length <= 0) return false;    const root = sequence[length - 1];    // 左子树节点的值小于根节点的值    let leftIndex = 0;    for (; leftIndex < length - 1; leftIndex++) {      if (sequence[leftIndex] > root) {        break;      }    }    // 右子树节点的值大于根节点的值    let rightIndex = leftIndex;    for (; rightIndex < length - 1; rightIndex++) {      if (sequence[rightIndex] < root) {        return false;      }    }    // 判断左子树是否为二叉树    let leftVerify = true;    if (leftIndex > 0) {      leftVerify = this.verifySequenceOfBST(sequence, leftIndex);    }    let rightVerify = true;    if (leftIndex < length - 1) {      rightVerify = this.verifySequenceOfBST(        sequence.slice(leftIndex + 1),        length - leftIndex - 1      );    }    return leftVerify && rightVerify;  }

测试用例

接下来我们将思路分析中所列举的例子代入上述代码，来验证下我们的代码能否正确执行。

const arr = [5, 7, 6, 9, 11, 10, 8];console.log("比对结果", treeOperateTest.verifySequenceOfBST(arr, arr.length));

我们再列举一个错误的例子，来验证下它能否正确判断。

const arr = [7, 4, 6, 5];console.log("比对结果", treeOperateTest.verifySequenceOfBST(arr, arr.length));

示例代码

本文用到的代码完整版请移步：

• TreeOperate.ts
• TreeOperate-test.ts

写在最后

至此，文章就分享完毕了。

我是神奇的程序员，一位前端开发工程师。

如果你对我感兴趣，请移步我的个人网站，进一步了解。

• 文中如有错误，欢迎在评论区指正，如果这篇文章帮到了你，欢迎点赞和关注😊
• 本文首发于神奇的程序员公众号，未经许可禁止转载💌