这几天看了几个智能算法,并且试着自己写了下,个人感觉这几个算法有许多的相似之处,那就是都是通过某种随机函数来对已有结果进行改变,建立某种评估函数(如适应度函数),然后再通过某种函数对其进行筛选,并将前两者循环多次,即可得到优化后的值。

智能算法在大多数的情况下都只能得到最优解的近似值,并且可能会陷入到局部最优解当中。

模拟退火算法

模拟退火算法总的来说还是一种优化算法,就如同名称一样,打铁后,钢铁冷却的过程就是其逐渐成形的过程. 模拟的是淬火冶炼的一个过程,通过升温增强分子的热运动,然后再慢慢降温,使其达到稳定的状态。 当温度很高时,钢铁容易发生形变,因此我们可以将其塑造成我们想要的形状;而当温度逐渐降低时,钢铁发生形变的容易程度降低,更加的趋向于稳定.

模拟退火算法的关键解释：

建立初始解
通常是以一个随机解作为初始解. 并保证理论上能够生成解空间中任意的解,也可以是一个经挑选过的较好的解,初始解不宜“太好”, 否则很难从这个解的邻域跳出,针对问题去分析。
生成扰动邻解
邻解生成函数应尽可能保证产生的侯选解能够遍布解空间,邻域应尽可能的小,能够在少量循环步中允分探测.,但每次的改变不应该引起太大的变化。
Metropolis准则
Metropolis法则是SA接受新解(扰动邻解)的概率。

$$ P(x=>x')=\begin{cases} 1 & f(x')<f(x) \ e^{-\dfrac{f(x')-f(x)}{T}} & f(x')>=f(x) \end{cases} $$

注:x表示当前解,x'为新解,这也是模拟退火区别于贪心的一点,我们在更新新解的时候对于不满足条件的情况,我们也有一定的概率来进行选取,从而可以使得退火模拟可以跳出局部最优解.
降温公式
经典模拟退火算法的降温方式：

$$ T(t)=\dfrac{T_0}{log(1+t)} $$

快速模拟退火算法的降温方式:

$$ T(t)=\dfrac{T_0}{1+t} $$

常用的模拟退火算法的降温方式还有(通常0.8<α<0.99):

$$ T(t+\Delta{t})=\alpha{T(t)} $$

终止条件自己设定阈值即可。

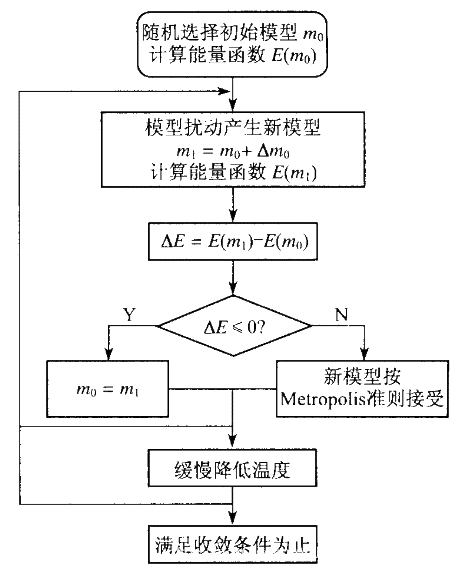
模拟退火算法流程

1. 初始化,温度T,任取一个初始解S1
2. 对当前温度T和k=1,2,…,L,重复步骤(3)~(6)
3. 对于当前的Si通过某种函数随机产生一个新解Si+1
4. 计算Si+1的花费增量df=f(Si+1)-f(Si),f为代价函数
5. 如果df<0,则用Si+1代替Si；否则按照exp(-df/T)的概率来决定是否用Si+1代替Si,（Metropolis准则）
6. 如果满足终止条件则退出,否则温度T衰减,返回步骤2

流程图如下：

粒子群算法

粒子群算法的关键解释：

建立初始解
首先，我们需要设置最大的速度区间，防止超出最大的区间。位置信息即为整个搜索空间，我们在速度区间和搜索空间上随机初始化速度和位置。设置群体规模。

求个体极值与全局最优解
个体极值为每个粒子找到的历史上最优的位置信息，并从这些个体历史最优解中找到一个全局最优解，并与历史最优解比较，选出最佳的作为当前的历史最优解。

更新速度和位置的公式
更新公式为:

$$ V_{id}=\omega{V_{id}}+C_{1}random(0,1)(P_{id}-X_{id})+C_{2}random(0,1)(P_{id}-X_{id}) \ X_{id}=X_{id}+V_{id} $$

算法的流程图如下:

其中，$\omega$称为惯性因子，$C_{1}$和$C_2$称为加速常数，一般取$C_{1}=C_{2}\in[0,4]$。$random(0,1)$表示区间上的随机数。$P_{id}$表示第$i$个变量的个体极值的第$d$维。$P_{gd}$表示全局最优解的第$d$维。

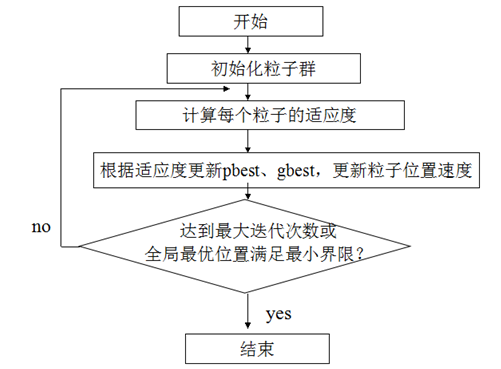
1. 初始化n个粒子的种群,初始化每个粒子的速度,位置
2. 设定最大速度Vmax
3. 计算每个个体的适应度,求得当前最优解
4. 根据最优解的位置,对每个粒子进行演化计算,算出每个粒子的速度(带方向)
5. 更具每个粒子的速度更新粒子的位置
6. 如果终止条件满足,则退出,否则返回3

流程图如下:

鱼群算法

算法流程描述如下:

1. 初始化设置,包括种群规模N、每条人工鱼的初始位置、人工鱼的视野Visual、步长step、拥挤度因子δ、重复次数T；
2. 计算初始鱼群各个体的适应值,取最优人工鱼状态及其值赋予Best；
3. 对每个个体进行评价Food Consistence,对其要执行的行为进行选择,包括觅食Pray、聚群Swarm、追尾Follow和随机行为；
4. 执行人工鱼的行为,更新自己,生成新鱼群；
5. 评价所有个体。若某个体优于Best ,则将Best更新为该个体；
6. 当满足终止条件时结束,否则转3

鱼群的个体行为

• 觅食行为：一般情况下鱼在水中随机地自由游动,当发现食物时,则会向食物逐渐增多的方向快速游去

• 聚群行为: 鱼在游动过程中为了保证自身的生存和躲避危害会自然地聚集成群,鱼聚群时所遵守的规则有三条:
  -- 分隔规则：尽量避免与临近伙伴过于拥挤;
  -- 对准规则：尽量与临近伙伴的平均方向一致;
  -- 内聚规则：尽量朝临近伙伴的中心移动。

• 追尾行为：当鱼群中的一条或几条鱼发现食物时,其临近的伙伴会尾随其快速到达食物点

• 随机行为：单独的鱼在水中通常都是随机游动的,这是为了更大范围地寻找食物点或身边的伙伴

以上三种算法的代码见我的GIthub仓库:https://github.com/Kingfish404/Algorithm