python 曲线拟合方法
背景
有些产品可能需要用到旋钮来调节音量,比如对讲机,收音机等。如何实现呢?常见的一种实现方案是使用电位器接一个ADC输入,通过ADC检测电压的大小变化来调节音量大小,软件实现上需要定时检测ADC的电压变化,检测周期长短影响音量调节体验,设置的周期长,反应速度慢,会出现突然声音大或者突然声音小的情况,检测时间太频繁,系统又会频繁唤醒,无法进入低功耗状态。
另一种方式是是使用旋转编码器接几个GPIO,通过旋转编码器可以检测到正转反转,通过其输出信号可以得到旋转角度。
电位器实物图:

旋转编码器实物图:

在某项目中使用ADC+可调电位器的方式实现音量调节功能,电路如下图:
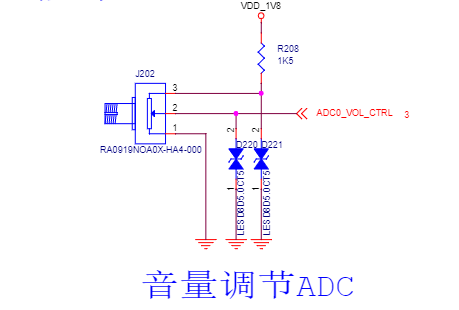
在使用ADC时发现一个问题,从ADC读取到的电压值并不是实际电压,从ADC读取的电压值范围是0~184mv,测量得到的实际电压为0~1668mv,所以需要对ADC的原始数据做处理,通过软件拟合得到真实电压。遇到问题,解决问题,学习使用python处理曲线拟合的几种方法。
python 调试环境介绍
对我的python开发调试环境做个简单介绍,操作系统是win 10,安装的python 是3.8,同时安装了 jupyter lab。
平时一些简单的python脚本编写、算法验证通常都是在 jupyter lab环境上编码调试。
为什么使用jupyter lab呢?
python对我来说是一门辅助性的工具,通常编写的代码量不大,jupyter lab 上可以运行代码,绘图显示方便,同时编写笔记,所以jupyter lab 非常适合我的使用需求,而不需要重量级的IDE开发环境。
下面是一个来自jupyter lab官网的运行界面图,除了支持python,还支持c++、R、Julia等其他编程语言。
python 线性拟合方法
线性拟合需要用到的python包有 numpy、matplotlib 和 scipy,通过pip安装即可,然后导入需要用到的python包
|
|
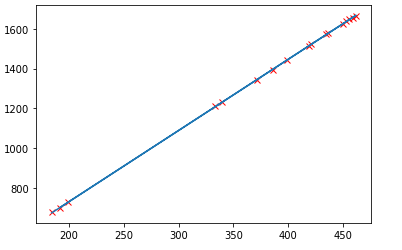
导入从adc读取到的原始数据和实际测量得到的电量数据,数据量不大,定义为列表,然后绘制ADC原始数据和实际电压的曲线图。
|
|
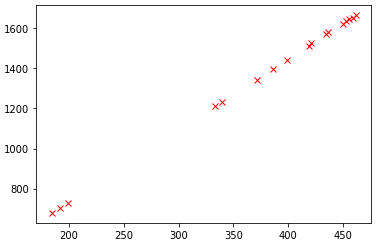
从上图看,原始数据和实际电压数据基本上保持线性关系,这是比较幸运的情况,从图上看应该是一条直线,通过直线拟合的方法来得到实际电压没有问题。
怎么获取这条直线的参数呢?
方法1,numpy 提供的多项式拟合函数polyfit计算。
线性拟合为一阶多项式,一阶多项式$$y = a_1 x + a_0$$拟合成功返回两个系数 $$[a_1, a_0]$$。
|
|
使用poly1d生成多项式函数。
|
|
然后画出拟合曲线图。
|
|
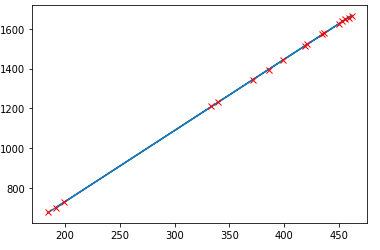
方法2,使用scipy提供的线性回归函数linregress求解
|
|
绘制拟合曲线图
|
|
方法3,求最小二乘解
当使用一个 N-1 阶的多项式拟合这 M 个点时,有这样的关系存在$$XC = Y$$ ,
$$\left[ \begin{matrix} x_0^{N-1} & \dots & x_0 & 1 \\ x_1^{N-1} & \dots & x_1 & 1 \\ \dots & \dots & \dots & \dots \\ x_M^{N-1} & \dots & x_M & 1 \end{matrix}\right] \left[ \begin{matrix} C_{N-1} \\ \dots \\ C_1 \\ C_0 \end{matrix} \right] = \left[ \begin{matrix} y_0 \\ y_1 \\ \dots \\ y_M \end{matrix} \right]$$
使用一阶多项式求解,即N=2,先将adc扩展为X,vo转换为Y:
|
|
求解:
|
|
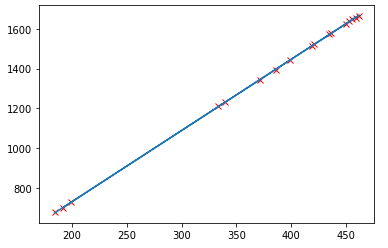
绘图:
|
|
非线性拟合
-
多项式拟合正弦函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20# 定义sin函数 x = np.linspace(-3 * np.pi,3 * np.pi,100) y = np.sin(x) # 多项式拟合,从一阶多项式到9阶多项式 y1 = poly1d(polyfit(x,y,1)) y3 = poly1d(polyfit(x,y,3)) y5 = poly1d(polyfit(x,y,5)) y7 = poly1d(polyfit(x,y,7)) y9 = poly1d(polyfit(x,y,9)) # 绘图 p = plt.plot(x, y, 'k-') p = plt.plot(x, y1(x)) p = plt.plot(x, y3(x)) p = plt.plot(x, y5(x)) p = plt.plot(x, y7(x)) p = plt.plot(x, y9(x),"g--") a = plt.axis([-3 * np.pi, 3 * np.pi, -1.25, 1.25])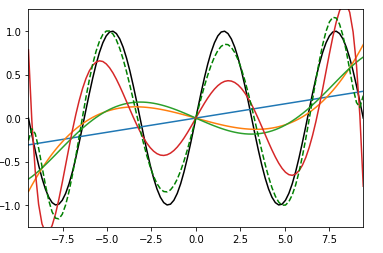
-
拟合自定义曲线
$$y = a e^{-b sin( f x + \phi)}$$
定义非线性函数:
1 2 3 4def function(x, a , b, f, phi): """a function of x with four parameters""" result = a * np.exp(-b * np.sin(f * x + phi)) return result1 2 3 4 5 6 7 8 9 10 11from scipy.optimize import curve_fit from scipy.stats import norm # 绘制原始曲线和加入噪声后曲线 x = np.linspace(0, 2 * np.pi, 50) actual_parameters = [3, 2, 1.25, np.pi / 4] y = function(x, *actual_parameters) y_noisy = y+ 1.8 * norm.rvs(size=len(x)) p = plt.plot(x, y, 'k-') p = plt.plot(x, y_noisy, 'gx')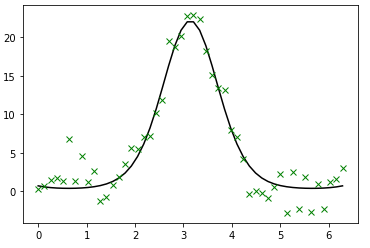
使用curve_fit求解
1 2 3 4 5 6 7p_est, err_est = curve_fit(function, x, y_noisy) # 第一个返回的是函数的参数,第二个返回值为各个参数的协方差矩阵 # 绘制结果曲线 p = plt.plot(x, y_noisy, "gx") p = plt.plot(x, y, 'k') p = plt.plot(x, function(x, *p_est), "r")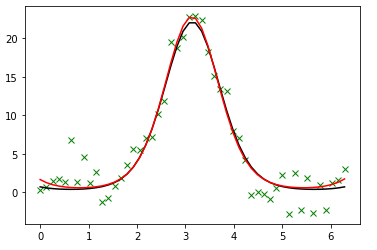
参考资料