关于(零知识)计算复杂性的总结
春秋十二月发表于 2024-02-09 14:19:00
经典的复杂性关系
P是多项式时间确定型图灵机可识别的语言类,NP是多项式时间非确定型图灵机可识别的语言类,NPC表示NP完全问题类,coNP表示NP的补,coNPC表示NPC的补。确定型图灵机是一种从不选择移动的特殊的非确定型图灵机,故自然有P属于NP
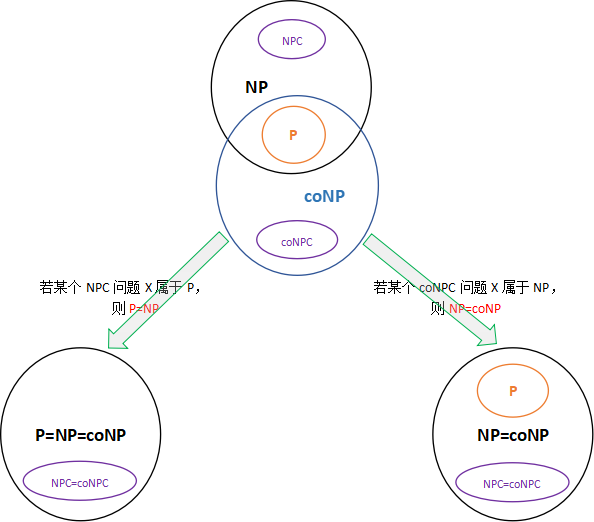
coNP、coNPC的定义之集合表述
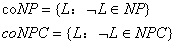
上面顶部的图有个假设前提是:coNPC不属于NP,即我们相信NP完全问题的补都不属于NP。但当P=NP或NP=coNP时,可以发现coNPC属于NP
◆ 为什么coNPC属于coNP?
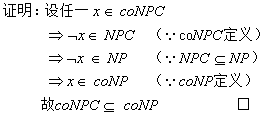
◆ 为什么NPC 不属于coNP?

◆ 为什么P属于coNP?
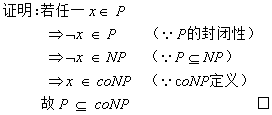
◆ 当P=NP时,为什么NP=coNP?

◆ 当NP=coNP时,为什么NPC=coNPC?


P是多项式时间确定型图灵机可识别的语言类,NP是多项式时间非确定型图灵机可识别的语言类,NPC表示NP完全问题类,coNP表示NP的补,coNPC表示NPC的补。确定型图灵机是一种从不选择移动的特殊的非确定型图灵机,故自然有P属于NP

coNP、coNPC的定义之集合表述
上面顶部的图有个假设前提是:coNPC不属于NP,即我们相信NP完全问题的补都不属于NP。但当P=NP或NP=coNP时,可以发现coNPC属于NP
◆ 为什么coNPC属于coNP?
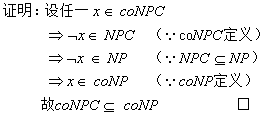
◆ 为什么NPC 不属于coNP?

◆ 为什么P属于coNP?
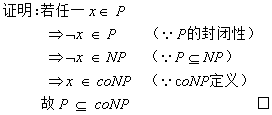
◆ 当P=NP时,为什么NP=coNP?

◆ 当NP=coNP时,为什么NPC=coNPC?

前文的关系演变图没考虑多项式空间问题类PS与递归问题类(因为那两个条件不会影响到它们),PS(NPS)是带多项式空间限制的确定型(非确定型)图灵机可接受的语言类,但不限制运行时间可能需超多项式或指数时间,在外围加上PS与递归语言类后如下
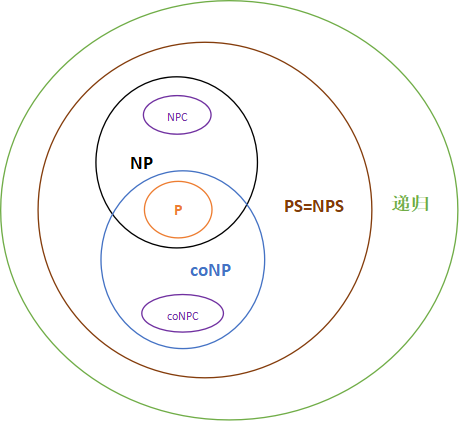
◆ 为什么coNP 属于PS?

零知识复杂性关系

BPP是可被概率多项式时间图灵机(即随机化算法)识别的语言类,IP是所有具有交互证明系统的语言构成的类,等于多项式空间语言类即前文经典复杂性关系中的PS,如下图所述

SZK!=CZK是因为计算不可分辨不一定能推出统计不可分辨,BPP!=PZK之原因可理解为BPP是退化的特殊的完备交互证明系统(证明者什么都不做,仅由验证者概率性地决定是否接受或拒绝)。
当(非均匀)单向函数存在时CZK=IP,涉及的命题与定理如下



也就是说PS类中的每种语言都具有零知识证明系统,比如NP有如下构造


◆ 为什么coNP 属于PS?

零知识复杂性关系

BPP是可被概率多项式时间图灵机(即随机化算法)识别的语言类,IP是所有具有交互证明系统的语言构成的类,等于多项式空间语言类即前文经典复杂性关系中的PS,如下图所述

SZK!=CZK是因为计算不可分辨不一定能推出统计不可分辨,BPP!=PZK之原因可理解为BPP是退化的特殊的完备交互证明系统(证明者什么都不做,仅由验证者概率性地决定是否接受或拒绝)。
当(非均匀)单向函数存在时CZK=IP,涉及的命题与定理如下



也就是说PS类中的每种语言都具有零知识证明系统,比如NP有如下构造
