Blum数的基本定理及应用
春秋十二月发表于 2024-02-25 15:29:00
【定义】设整数N=P×Q,P与Q皆为素数,如果P≡Q≡3 (mod4),则N为一个Blum(布卢姆)数
【定理】设N为Blum数,N ∤ d,若同余方程x2≡d (mod N)有解,则d的平方根中有一半的Jacobi符号为1,另一半Jacobi符号为-1;且仅有一个平方根为模N的二次剩余

【推论】设N为Blum数,N=P*Q,令
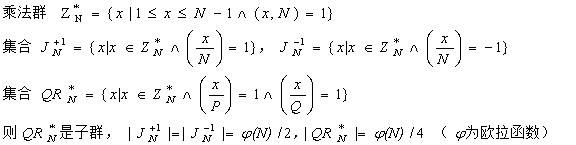
证明:
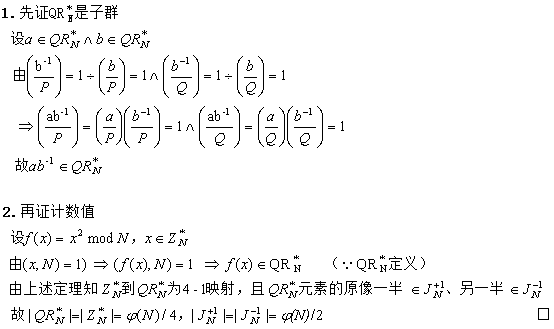
【应用】Blum-Goldwasser公钥加密

解密正确性是因为步骤1用到了欧拉定理及求平方根的如下算法,步骤2用到了中国剩余定理


从上可得x=s(P+1)/4 mod P或x=P-s(P+1)/4 mod P,因(-1)(P-1)/2等于-1 mod P,故前者为模P的二次剩余。
所以从密文中r求它的(p+1)/4次幂、(q+1)/4次幂,迭代n次就得到了s1模p的解、s1模q的解,又因p、q、n在迭代中不变,故用欧拉定理预计算dp mod (p-1)、dq mod (q-1)
所以从密文中r求它的(p+1)/4次幂、(q+1)/4次幂,迭代n次就得到了s1模p的解、s1模q的解,又因p、q、n在迭代中不变,故用欧拉定理预计算dp mod (p-1)、dq mod (q-1)