IT博客汇 | 使用一条MySQL SQL语句完成24点计算

使用一条MySQL SQL语句完成24点计算

admin发表于 2024-03-30 11:53:11

概述

最近，组织了一个24点SQL编程的比赛，笔者是主办方，也是评委。既然是做评委，自己也先挑战了一下，因为对MySQL更为熟悉，故选择了MySQL作为编程SQL。周末花了一些时间挑战一下，这里记录一下自己的解法以及思路。

24点问题，是一个有趣的问题。他的扩展问题（即把牌数/计算值进行更改），很可能也是一个NP-完全问题，他与subset sum problem问题有一些些类似。如果参考subset sum problem问题的解法（例如做一些动态优化解），则可以实现还比较优的解。

不过，这一次的比赛，是要求在一条SQL里面实现，并且限制了SQL长度为10KB，所以就大大限制了实现的方式。不过最为直接的两个思路还是，“暴力的枚举”计算和“预计算结果再做哈希求解”。即便如此，在写SQL过程中，还是遇到了如下挑战需要解决：

使用单条SQL进行暴力枚举的时候，如何在没有for/while等循环控制，如何遍历所有的可能性
哈希数组的空间占用比较大，可能会超过10KB，如何去压缩或者减少需要构建的数组

另外，实现过程中，可能涉及到浮点数计算、除数为零等问题的处理，也是非常容易出错的。

另一个角度，这些，也是这道题，有趣的地方。

“一条SQL算24点”的题目回顾

这次的题目，与一般意义上24点略有一些不同：

首先，要求一条SQL内完成；对于穷举、哈希的实现本身就有挑战了。需要对SQL比较熟悉，否则很难写出正确、高性能的SQL
SQL大小限制为10KB，所以，并不能简单的穷举，简单的CASE WHEN 10KB肯定是不够的
4个数字，被限制为1~10，而不是13，所以搜索空间是相对来说少了一些的，让10KB以内哈希成为可能

详细赛题：参考

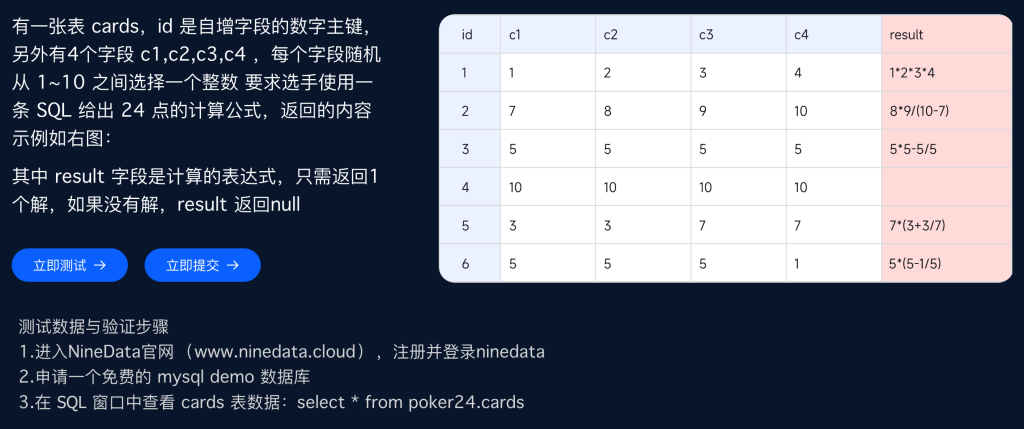
初始化数据

4张牌，每张牌取值为1~10，所以一共10000中可能，使用SQL构建存储如下：

CREATE TABLE cards(
    id int auto_increment primary key,
    c1 int ,
    c2 int, 
    c3 int, 
    c4 int
);

INSERT INTO cards(c1,c2,c3,c4) 
    WITH RECURSIVE seq(n) as 
    (
        select 1
        union 
        select n+1 from seq where n<=9
    )
    select t_1.n,t_2.n,t_3.n,t_4.n
    from 
        seq as t_1,
        seq as t_2,
        seq as t_3,
        seq as t_4

这次一共实现了两种算法，一个是正统的枚举计算，一个是结果倒推的哈希解法。我们先看看如何使用一条SQL实现正统的枚举计算。

一条SQL的正统（“暴力”）枚举计算

完整的SQL参考：https://www.orczhou.com/24.v1.txt 。如果对这条SQL比较困惑的话，又对这个问题有兴趣的话，可以继续阅读。

解题思路说明

使用二叉树表达表达式。枚举的搜索空间还是非常大的，如果使用二叉树来表示24点计算结果的话，完整的会有五种形式的树：left-most、right-most和3种bushy的树。
使用JOIN的方式来实现枚举。例如，要枚举所有的三个运算符，每个运算符有四种可能（”+-*/”），那么可以使用一张表，该表共三个字段“op_1st、op_2nd、op_3rd”，共4*4*4条记录，每条记录是一种表达式的组合。然后使用该表去与原（cards）进行JOIN。
需要枚举的除了上面提到的运算符，还有四个数字的顺序，例如，一条cards表的记录有四个数字：c1、c2、c3、c4；那么，在枚举表达式 (c1 / (c2 – c3) )- c4 时，(c2 / (c1 – c3) )- c4等情况也需要考虑，这种情况的数量是4*3*2 = 12种。实现的方式，与上面操作符枚举类似，构建一个表，例如叫full_order，把所有可能得顺序都枚举一遍，然后与原表（cards）进行JOIN。具体的full_order表有四个字段c_[1-4]，每个字段取值为[1-4]，且两两不同，那么这个表就代表了所有的c1、c2、c3、c4的顺序可能。
有了上面三种分析，那么对于一组数字，所有需要枚举的可能性是：5棵树*4*4*4种运算符组合*4*3*2种顺序组合，即7680种组合。

二叉树表达式分析

这大概很多人会遇到的是第一个“难”题，也注意到很多人在实现的时候，虽然能够枚举部分表达式，但是非常容易遗漏。另外，也因为搜索空间很大，所以，实现细节上也很容易出错。这里使用基础的编译原理知识可以知道，一个表达式与“一种树”结构是一一对应的，而这样的树一共有五种。

我们来看一个例子： ((c1*c2)+c3)*c4。那么它对应树形结构如下：

               ((c1*c2)+c3)*c4       ((c1 op_1st c2) op_2nd c3) op_3rd c4
                     <*>                             <op_1st>
                      |                                 |
                ------------                      ------------
                |          |                      |          |
               <+>        c4                   <op_2nd>      c4
                |                                 |
         --------------                    --------------
         |            |                    |            |
        <*>           c3                <op_3rd>        c3
         |                                 |
   ------------                      ------------
   |          |                      |          |
  c1          c2                    c1          c2

那么对于任意一组数字（c1,c2,c3,c4）一共有多少种这样的树呢？答案是五种，这里不一一详述，每种树对应的表达式如下，这了使用op_1、op_2、op_3代表“+-*/”中的任意一种运算符：

((c1 op_1 c2) op_2 c3) op_3 c4 即上面的左深树
c1 op_1 (c2 op_2 (c3 op_3 c4)) 右深树
(c1 op_1 c2) op_2 (c3 op_3 c4) bushy树
c1 op_1 ((c2 op_2 c3) op_3 c4) bushy树
(c1 op_1 (c2 op_2 c3)) op_3 c4 bushy树

大家可以用上面的树形图画一下五种树，就比较好理解了。

每种树的可能性枚举

对于上述的每一棵树，都有三个“操作符”和“四个操作数”，这三个操作符都有4中选择（“+-*/”），四个操作数的选择空间要小一些，因为不能重复，不过根据简单的排列组合知识可以有：(4*4*4)*(4*3*2*1)种可能性。

再与上面的5种树组合，一共有 5*(4*4*4)*(4*3*2*1)=7680种组合。

重复的树

这里的树的种类看起来非常多，但是因为加法和乘法有交换律、结合律，以及减法有去括号的方法，所以，“等价的树”非常多。去掉等价的树，能够把这个搜索空间大幅度缩小。那么问题来了：理论上，去掉所有重复（“等价”）的树，最后剩余的数量是多少？(这似乎并不是一个简单的问题，不过不属于本文讨论的内容）。

在很多的算法优化里面，如果能够尽可能多的把这些“等价”树砍掉，就可以大大提升执行的效率。事实上，这次解题中，公司有个同事比较极限，在上面的问题中，把这些树的枚举可能性砍到了非常小。当然，因为是限制在这道题中，很多树可能是无效的（虽然没有等价树，但是可能计算中并不需要使用）。

一般的，等价的树包括了：

加法、乘法的交换律会导致大量的重复树
加法、乘法的结合律，也会导致很多的重复的树
减法和除法的去括号等价变化（例如c1-(c2-c3)与c1-c2+c3）

在这里的中，暂时没有考虑这些等价树的消除。

操作符的遍历SQL实现

如前所述，每颗树共有三个操作符，都可以是“+-*/”中的任何一个，这里使用MySQL的CTE（WITH/Common Table Expressions）功能和JOIN功能实现枚举和遍历：

(
    WITH op_list (op) as (
        SELECT '*'
        UNION
        SELECT '+'
        UNION
        SELECT '-'
        UNION
        SELECT '/'
    )
    SELECT
        op_1.op as op_1st,
        op_2.op as op_2nd,
        op_3.op as op_3rd
    FROM
        op_list as op_1,
        op_list as op_2,
        op_list as op_3
) full_op

“操作数”顺序的枚举

每一颗树都有四个“操作数”，每个操作数都是{c1,c2,c3,c4}中的一个，但不重复（这里的不重复是指不能出现c1 c1 c3 c4这四个数字每个用一遍，但需要注意c1 c2 c3 c4本身是可能有重复的数字的，例如 3,3,5,8的数字组合）。现在需要把四个操作数的所有组合（4*3*2种）全部都枚举出来。这里使用行转列后，再使用4个顺序表的方式实现：

为了实现4个操作的不重复的组合，这里使用了如下方法：

          (
              WITH RECURSIVE seq (n) as (
              SELECT 1
              UNION ALL
              SELECT n + 1 FROM seq WHERE n <= 3
          )
          select
              seq_1.n as seq_num_1,
              seq_2.n as seq_num_2,
              seq_3.n as seq_num_3,
              seq_4.n as seq_num_4
          from
              seq as seq_1,
              seq as seq_2,
              seq as seq_3,
              seq as seq_4
          WHERE
              pow(2,seq_1.n-1)+pow(2,seq_2.n-1)+pow(2,seq_3.n-1)+pow(2,seq_4.n-1) = 15
          ) full_order

到这里，full_order表就可以表示所有的排列组合了。但是如何利用full_order表的四个列seq_1、seq_2、seq_3、seq_4来把{c1,c2,c3,c3}都枚举出来，还需要做一些转换。这个转换要在SELECT中的item list部分。即：

SELECT 
    item_list
FROM 
    cards,
    (...) as full_order
    (...) as full_op

在iteml_list部分，需要对c1,c2,c3,c4按照full_order进行重新排序处理，这里是略有一些复杂的：

SELECT 
        ...
        @c_1 := case full_order.seq_num_1 
            when 1 then c1 
            when 2 then c2 
            when 3 then c3 
            when 4 then c4 
        END as c_1,
        @c_2 := case full_order.seq_num_2
            when 1 then c1 
            when 2 then c2 
            when 3 then c3 
            when 4 then c4 
        END as c_2,
        @c_3 := case full_order.seq_num_3
            when 1 then c1 
            when 2 then c2 
            when 3 then c3 
            when 4 then c4 
        END as c_3,
        @c_4 := case full_order.seq_num_4
            when 1 then c1 
            when 2 then c2 
            when 3 then c3 
            when 4 then c4 
        END as c_4,
        ...
FROM 
    cards,
    (...) as full_order
    (...) as full_op

五种“表达式树”的计算

在前面的小结“二叉树表达式分析”中，已经对五种表达式进行了分析。对于表达式中使用的“操作符”、“操作数”也已经准备好了。那么就需要逐一计算5中表达式了。这里也是用最“暴力”的方式，分别计算五棵树的表达式的值。

这里仅暂时left most tree的计算，如下：

        /* total 5 trees */   
        /*left most tree*/
        /* ((@c_1 op_1 @c_2) op_2 @c_3) op_3 @c_4  */
        @lt_1 := case op_1st 
            when '*' then @c_1 * @c_2
            when '+' then @c_1 + @c_2
            when '-' then @c_1 - @c_2
            when '/' then @c_1 / @c_2
        END as lt_1,
        
        @lt_2 := case op_2nd 
            when '*' then @lt_1 * @c_3
            when '+' then @lt_1 + @c_3
            when '-' then @lt_1 - @c_3
            when '/' then @lt_1 / @c_3
        END as lt_2,
        
        @lt_3 := case op_3rd 
            when '*' then @lt_2 * @c_4
            when '+' then @lt_2 + @c_4
            when '-' then @lt_2 - @c_4
            when '/' then @lt_2 / @c_4
        END as lt_3,
        
        @lt_expr := concat("((", @c_1 ,op_1st,@c_2 ,")",op_2nd,@c_3,")",op_3rd,@c_4),
        if(@lt_3 between 24-0.0001 and 24+0.0001, @if_found := true, 0),
        if(@lt_3 between 24-0.0001 and 24+0.0001, @r_expr := @lt_expr, 0),

浮点数的精度与除数为零的问题

这里有两个问题需要注意，也是在整个比赛过程中，很多选手都会犯错误的地方，其中一个是：

浮点数精度的问题

在很多算式的计算中会涉及到“无限循环小数”，而计算机在处理时，则会通过按照一定的精度近似。例如3、3、8、8的计算方法8/(3-8/3)。这个问题比看起来的更加隐蔽，在MySQL中，我们观察如下表达式：

mysql> select 8/(3-8/3),@i:=8/3,@j:=3-@i,@k:=8/@j;
+-----------+---------+-------------+--------------------+
| 8/(3-8/3) | @i:=8/3 | @j:=3-@i    | @k:=8/@j           |
+-----------+---------+-------------+--------------------+
|   24.0000 |  2.6667 | 0.333333334 | 23.999999952000003 |
+-----------+---------+-------------+--------------------+

可以看到，直接的计算8/(3-8/3)是可以算出24的，但分步骤计算，则会出错，所以，在实现时，如果是分步计算，则很容易会出现错误。

知道了错误在哪里，解决其实是比较简单的，在最终的计算结果做一次四舍五入，例如保留3位小数即可，即：

mysql> select 8/(3-8/3),@i:=8/3,@j:=3-@i,@k:=round(8/@j,4);
+-----------+---------+-------------+-------------------+
| 8/(3-8/3) | @i:=8/3 | @j:=3-@i    | @k:=round(8/@j,4) |
+-----------+---------+-------------+-------------------+
|   24.0000 |  2.6667 | 0.333333334 |           24.0000 |
+-----------+---------+-------------+-------------------+

也可以在结果判断的时候，再引入一次额外的比较即可。可以看下面的SQL：

mysql> select 8/(3-8/3),@i:=8/3,@j:=3-@i,@k:=8/@j,@k = 24,@k between 24-0.0001 and 24+0.0001\G
*************************** 1. row ***************************
                         8/(3-8/3): 24.0000
                           @i:=8/3: 2.6667
                          @j:=3-@i: 0.3333333340000002
                          @k:=8/@j: 23.999999951999985
                           @k = 24: 0
@k between 24-0.0001 and 24+0.0001: 1

另一个问题是“除数为零的问题”，这是一个问题，需要考虑到，但可能无需做额外的处理。在穷举的算法中，有很多是需要除以0的。在MySQL中，如果SELECT语句的话，除以零的表达式会返回NULL。在处理时，需要注意这个细节就可以了。

具体的，可以参考MySQL的文档（参考）：

For SELECT, division by zero returns NULL. Enabling ERROR_FOR_DIVISION_BY_ZERO causes a warning to be produced as well, regardless of whether strict mode is enabled.
参考

返回表达式

最后，对于一组数据，算出所有五棵树的取值后，最后看看有没有等于24的，或者其中之一等于24，就可以停止计算了，同时需要将该树所代表的表达式输出出来，以供后续使用。例如对于前面的left-most tree：

        /* total 5 trees */   
        /*left most tree*/
        /* ((@c_1 op_1 @c_2) op_2 @c_3) op_3 @c_4  */
        @lt_1 := case op_1st 
            when '*' then @c_1 * @c_2
            when '+' then @c_1 + @c_2
            when '-' then @c_1 - @c_2
            when '/' then @c_1 / @c_2
        END as lt_1,
        
        @lt_2 := case op_2nd 
            when '*' then @lt_1 * @c_3
            when '+' then @lt_1 + @c_3
            when '-' then @lt_1 - @c_3
            when '/' then @lt_1 / @c_3
        END as lt_2,
        
        @lt_3 := case op_3rd 
            when '*' then @lt_2 * @c_4
            when '+' then @lt_2 + @c_4
            when '-' then @lt_2 - @c_4
            when '/' then @lt_2 / @c_4
        END as lt_3,
        
        @lt_expr := concat("((", @c_1 ,op_1st,@c_2 ,")",op_2nd,@c_3,")",op_3rd,@c_4),
        if(@lt_3 between 24-0.0001 and 24+0.0001, @if_found := true, 0),
        if(@lt_3 between 24-0.0001 and 24+0.0001, @r_expr := @lt_expr, 0),

最后，组装需要的输出的列

这里没有什么特别需要强调的，最后按照题目中要求的，输出需要的列就可以了。

完整的SQL参考：https://www.orczhou.com/24.v1.txt 。

附录1：关于NP-complete问题

虽然没有人有严格的证明，不过感觉上，24点问题很可能是一个NP-完全问题。初步的感觉是，与子集求和问题（subset sum problem)很像。从解法上，也可以使用类似的“动态规划”的思路去求解。

这里简述一下什么是P问题，什么NP问题，什么是NP-完全问题。这是一个在计算复杂度分析领域的问题，P问题，是指可以在多项式时间内求解的问题；NP问题是指，这个问题的解（任意解/也可以是错误解）给出后，可以在多项式时间内验证，解的正确性。

“NP-完全问题”（NP-complete problem），是所有NP问题中，非常难的一类，它指的是，以其他所有的NP问题都可以再多项式时间内转化/规约为此类问题。著名的NP-完全问题包括：

“数独问题”
“魔方”
“八皇后问题”
子集求解问题
中国邮递员问题
旅行推销员问题（Travelling salesman problem）（本身是一个NP问题，给定图、长度，问是否存在更短路径的问题，就是一个NP-C问题）

此外，前面提到的子集求和问题，该问题（泛化）是一个NP问题，一些变种则是NP完全问题。例如，一个变种是这样的，给定一个包含若干整数的集合，问，是否存在某个子集，其和为零。

24点问题，与这个问题有一些“像”，24点问题，是，有一个集合有四个数字和四个运算，问，是否存在一种组合让其数字和运算符恰好算得24。不过，这个问题是否为NP-C问题，笔者并不能确定。