69. Sqrt(x)
Question
Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.
You must not use any built-in exponent function or operator.
- For example, do not use
pow(x, 0.5)in c++ orx ** 0.5in python.
Example 1:
Input: x = 4
Output: 2
Explanation: The square root of 4 is 2, so we return 2.
Example 2:
Input: x = 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
Algorithm
A easiest way to solve it is to utilize math. How you solve it in math just implement using code, that's code1.
Or if you see a loop for all numbers may be you can optimize it to a binary search. To find the number whose square is just smaller than the target in a sorted number list.
But there is a famous way called Newton's method, which is hard to think, take times to prove but easy to implement and a little bit faster.
One of the best and widely used methods to compute sqrt is Newton's Method. Here we'll implement the version without the seed trimming to keep things simple. However, seed trimming is a bit of math and lot of fun, so here is a link if you'd like to dive in.
Let's keep the mathematical proofs outside of the article and just use the textbook fact that the set
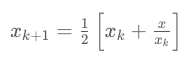
converges to $\sqrt{x}$ if $x_0=x$. Then the things are straightforward: define that error should be less than 1 and proceed iteratively.
Code1
class Solution { public int mySqrt(int x) { long res = 1; while (res * res <= x) { res++; } return (int) res - 1; } }
Code2
class Solution { public int mySqrt(int x) { long res = x; while (res * res > x) { res = (res + x / res) / 2; } return (int) res; } }
or
Code3
class Solution { public int mySqrt(int x) { if (x < 2) return x; double x0 = x; double x1 = (x0 + x / x0) / 2.0; while (Math.abs(x0 - x1) >= 1) { x0 = x1; x1 = (x0 + x / x0) / 2.0; } return (int)x1; } }