IT博客汇 | 随机梯度下降(SGD)和Mini-batch梯度下降

随机梯度下降(SGD)和Mini-batch梯度下降

admin发表于 2024-12-15 02:27:45

Mini-batch Gradient Descent的主要想法

在前面的实践中，使用“Gradient Descent”时，都是一次性把所有的数据集都考虑进去，一切似乎都没有什么问题。

但是，在现实实践中，如果训练数据量非常大，这种方式就不适用了。试想，在前面的示例中，输入样本数据，即\( X \)（或者 \( A^{[0]}\)），其维度（或者说shape）则可能是\( 300 \times 10,000,000 \)。这会导致每一次的梯度计算量都非常大，一次迭代（epoch）的时间会很长。

一种非常常见的、也是非常经典的梯度下降改进，就是 mini-batch gradient descent。首先，将样本分层若干小份，并单独对每个“小份”进行“Gradient Descent”，最后逐步完成所有样本的训练。完成一次所有样本的遍历，称之为一次迭代epoch。

在神经网络的训练中，可以用下面步骤理解这个过程：

for "a-small-batch-of-samples X^{t} " in "all-samples"
    forward  propagation on X^{t}
    backward propagation on X^{t}
    update W/b
        W^{[l]} = W^{[l]} - lr * dW^{[l]}
        b^{[l]} = b^{[l]} - lr * db^{[l]}

相对于 mini-batch gradient descent ，前面介绍的一次把所有样本都用于训练的方法，也被称为“batch gradient descent”。

Stochastic Gradient Descent

在 mini-batch 中，如果每次批量的样本大小是 1 的话，那么，也称为Stochastic Gradient Descent（简称 SGD,随机梯度下降）。事实上，自开始使用 Backpropagation 算法以来，SGD就被用于提升神经网络的训练的效率。并且很快的，mini-batch gradient descent 就作为一种优化被使用。目前，mini-batch gradient descent 依旧是一种常用神经网络训练方法^[1][2]。

收敛稳定性预估

不难想象，在“batch gradient descent”中，一次性把所有数据都用于梯度下降的算法，通常都能够获得更好的收敛速度。而在使用 mini-batch 的时候，由于不同的批次的样本在计算时，“计算梯度”都与“全局梯度”有一定的偏差，并且有时候偏差较大，有时候较小，所以，相比之下，收敛速度要慢一些。而，Stochastic Gradient Descent 则可能会更慢一些。

可以这么理解， mini-batch 和 Stochastic Gradient Descent 都总是使用一个局部的梯度（部分样本的梯度）来预估整体的梯度方向，自然效果会差一些。

这里我们改进了原来的神经网络实现 ssnn_bear.py，将其更新为使用 mini-batch 的 ssnn_cat.py。详细代码可以参考GitHub仓库：super simple neural network 。

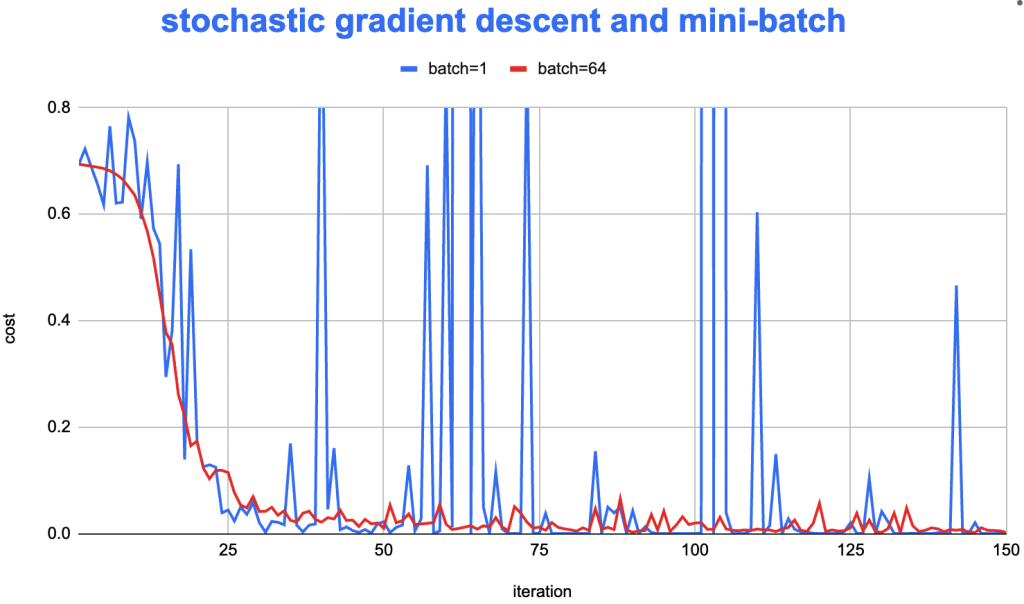
运行 ssnn_cat.py 并观察 mini-batch 的 cost 下降速度如下：

mini-batch 迭代下cost总是在上下波动

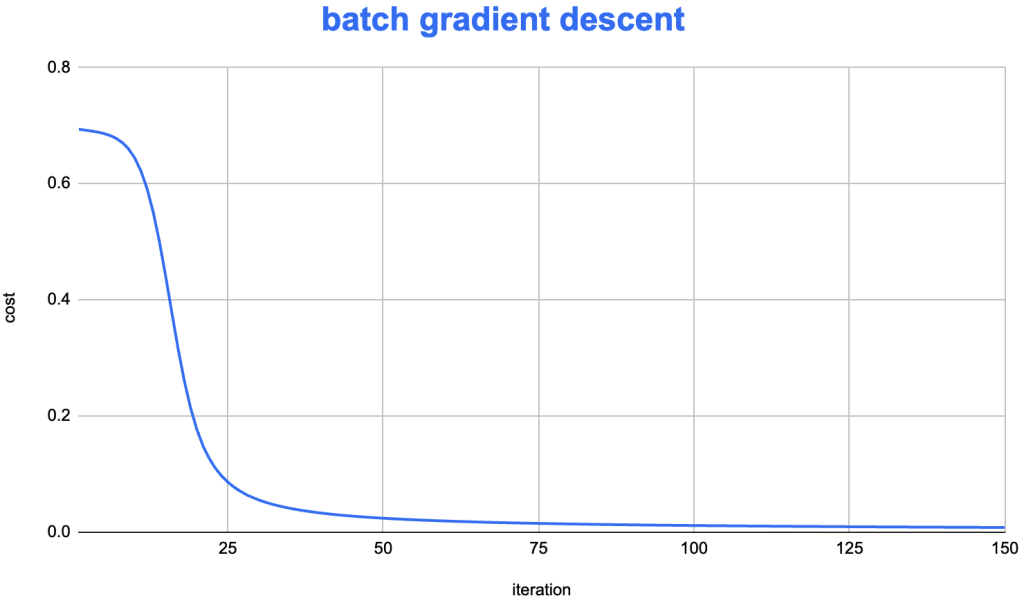
batch gd算法下cost下降非常稳定

batch_size 大小的配置

一些经验数值可能是64、128、256、512等。Mini-batch 需要在大数据量和向量化计算之间取得一个平衡，所以通常需要更具训练的设备选择合适的 batch 大小，使得每次迭代都充分利用硬件的资源。

代码实现

在前述的神经网络上（参考），再做了一些修改，实现了 Mini-Batch 或者随机梯度下降。

新增 batch 大小参数

首先，新增了 batch_size 参数表示，同时增加对应参数 batch_iteration 表示，在一次样本迭代中，总计需要循环多少次。所以，这两个参数有如下关系：

batch_iteration = math.ceil(m/batch_size)

对每批次样本做迭代

batch_iteration = math.ceil(m/batch_size)
...
for i in range(iteration_count):
    for i_batch in range(batch_iteration):
        ...
        # sample from i_batch*batch_size
        batch_from  = i_batch*batch_size
        batch_to    = min((i_batch+1)*batch_size,m)
        batch_count = batch_to - batch_from
        A0  = X[:,batch_from:batch_to] # column  [batch_from,batch_to)
        Y_L = Y[:,batch_from:batch_to] # Y_label [batch_from,batch_to)
        ...

代码的其他地方，几乎不需要太大的改动。完整的代码参考：ssnn_cat.py

参考

[1] Stochastic gradient descent
[2] https://github.com/orczhou/ssnn/blob/main/ssnn_cat.py
[3] https://github.com/orczhou/ssnn/blob/main/ssnn_bear.py
[4] https://github.com/orczhou/ssnn

这是一个系列文章包含了，完整的文章还包括：