大产品小细节!5分钟带你了解经典的费茨定律
金蝶云之家体验部交互设计师-王梓铭:大家有没有想过为什么按钮越大,越易于点击 ?为什么相关按钮需要相互靠近摆放 ?为什么 Win 系统要将「开始」按钮放在角落 ?这些设定的背后其实都有一个在人机交互中,非常重要的定律 —— 费茨定律。
上期回顾:《大产品小细节!5分钟了解格式塔原则》
一. 概述
首先来看看费茨定律公式:

看起来很复杂吧, 但实际上并不难,我用一张图给大家解释下费茨定律是什么。当用户需要拖动黄色点到目标区块中时:
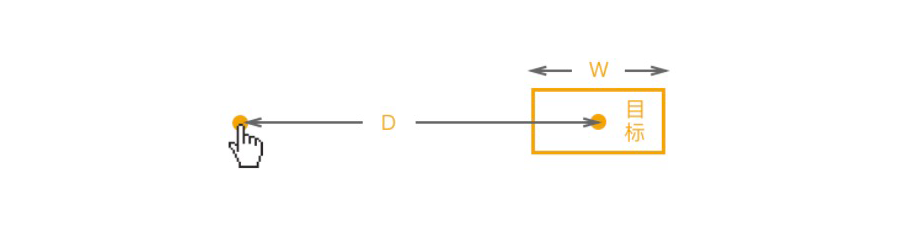
费茨定律中的 D 就是从开始点到目标中心的距离,而 W 则是目标的宽度大小。根据公式可以看到,A和 b 都是常量,那么 MT (黄点从左移到目标中心所需的时间)的大小取决于 D 和 W 的值:
- 当 D 一定时,W 越小,MT 越大;W 越大,MT 越小。
- 当 W 一定时,D 越小,MT 越小;D 越大,MT 越大。
解释一下就是:
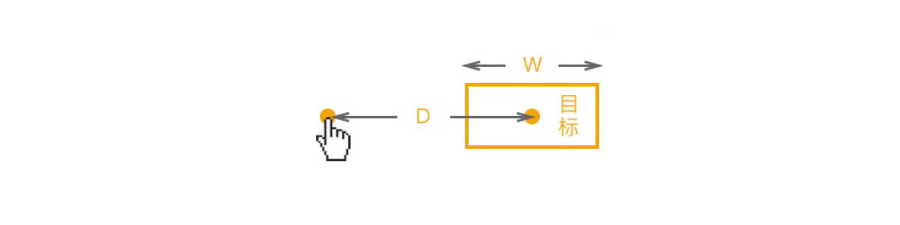
当距离一定时,目标越小,所花费的时间越长;目标越大,所花费的时间越短。(小而远的目标区域意味着用户需要将黄点移动较长距离,并且为了能对准目标还需要做一系列的微调,因为目标比较小嘛,所以耗费的时间自然就长了。)
当目标大小一定时,起点离目标中心的距离越近,所花费的时间越短;距离越远,所花时间越长。(这比较好理解,距离比较近嘛~ 所花时间自然比较短了。)
二. 启示与案例
按钮越大越易于点击
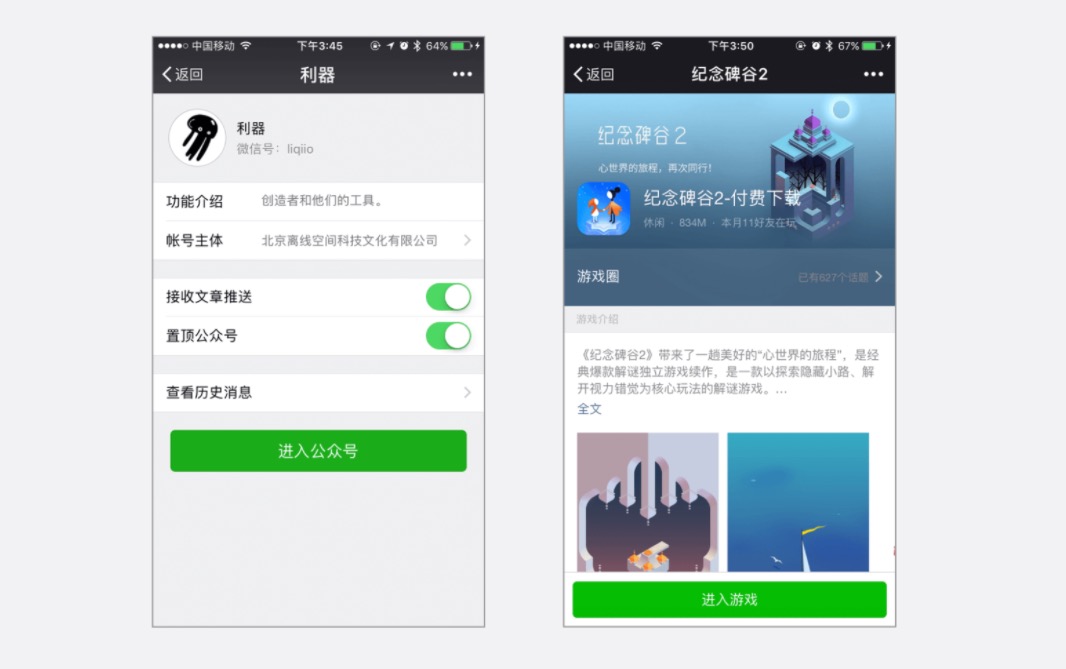
正如前面提到的,如果你想要让按钮的点击率更高可以尝试将按钮做大点,比如这样:
 将按钮放置在离开始点较近的地方
将按钮放置在离开始点较近的地方
还是拿上面两个界面为例子,大家有没有发现那两个大大的按钮是放在屏幕下方的?原因就是「将按钮放在底部可以使 D 变小」,要知道用户完成整个点击操作是要先将手指移动到目标上方,最后进行点击的。那么在这里 D 就是手指开始悬停的位置到目标上方的距离。根据研究表明,人们在使用手机的时候,75%的交互操作都是由拇指驱动的,而拇指悬停的位置恰恰就是屏幕下方。
PS:关于用户是如何使用触屏设备的,欢迎大家看看这篇读书笔记——「阅读」触类旁通:多终端时代的触屏界面设计 文中提到的书本,也推荐大家买来看看。
那么对于 PC 端设备,又是如何使用这一定律的呢?
最常见的使用就是鼠标右键操作了。点击右键,鼠标的右下或右上方就会出现一个菜单,鼠标移动到对应按钮上,点击一下即可完成操作。
相关按钮之间距离近点更易于点击
对于一些相关性较强的按钮,可以考虑将他们放在一起,比如:
- 在设计 PC 端的翻页按钮时,就可以将「上一页」和「下一页」放在互相靠近的位置。
- 在设计注册、登录界面的时候,可以将「注册」和「登录」放到一起,如果想要突出「注册」则可以考虑将「注册」按钮做大点。
- 相关联的操作也可以尝试放在一起,不仅可以在视觉上增强用户对他们相关性的认知,还可以减少在他们之间的距离 D。
无限大的四角与四边
文章开头,我提出了一个疑问:
为什么 Win 系统要将「开始」按钮放在角落 ?
原因就是屏幕的四角和四边 W 无限大,W 无限大的话,MT 就很小了。像 Mac 的 Docker 更是将费茨定律发挥得淋漓尽致,当鼠标 hover 到对应的 App icon 上的时候,icon 还会放大,从而加大 App icon 的W 。
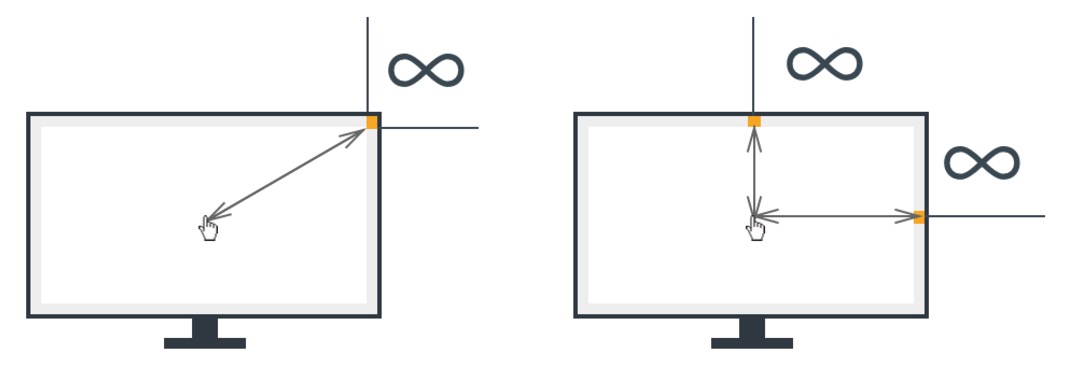 估计大家又会有个疑惑,那就是——为什么四角和四边的 W 无限大?
估计大家又会有个疑惑,那就是——为什么四角和四边的 W 无限大?
那是因为光标没法移动到四角与四边之外的地方,你再怎么移动鼠标,光标也没办法移到屏幕以外的地方,所以他们就进入到了「无限可选中」状态。
但是,随着屏幕尺寸越来越大,而且双屏幕的配置越来越常见,这个设计也变没得那么好用了,因为 D 变大了。同理手机端的四角与四边也是「无限可选中」位置,因为手点击屏幕以外屏幕不会响应嘛。(所以各位可以发现左上角按钮一般为返回,右上角为确定)但是在手机上时候,依然会面临屏幕越来越大,按钮越来越不好点击的问题。
三. 小练习
最后,我想跟大家一起做个小练习,那就是请大家和我一起设计手机的关机界面。
明确设计目标
首先明确设计目标:设计手机的关机界面。
明确约束与限制
明确了设计目标后,需要考虑设计约束与技术限制有哪些?(这里我们不考虑技术问题)对于关机操作来说,本身是个非常高危的操作,一经生效就没法撤销了。那么这里的设计约束就有:
- 此操作不能过于便捷
- 防止误触
- 如有必要需要有防待操作
将理论应用到设计中
根据约束,我们开始设计方案。在设计时候,我们不妨将我们所学的费茨定律应用到设计之中,估计这里又有同学会问,费茨定律不是教我们设计出易于点击的设计吗?很明显与你提到的约束相违背啊。其实费茨定律不只能正着用,还能反着用。比如我们可以尝试加大 D 和降低 W。

先尝试加大拇指到目标的距离 D,那么可以得出甲方案。(这设计就是很多安卓手机提供的的方案)
不过正如前面提到的第三条启示,相关的按钮放在一起更便于点击。但是我们实际上并不想让用户点击「关闭手机」而是希望用户点击「取消」,将两个放在一起并不合适,那么我们可以尝试降低「取消」按钮的 D 从而削弱用户点击「关闭手机」的可能,并且根据费茨定律我们可以将「关闭手机」的 W 做小,从而得出乙方案。
但是这个方案还不够极致,这里我想跟大家明确另一点:D 的距离是可以创造出来的。
触屏的伟大之处就在于,它不仅仅有点击操作,还有滑动操作。通过滑动操作也可以创造出 D 出来。如丙方案所示,完成关机操作的总 D 等于「大拇指移动到顶部滑块的距离」加上「按住滑块滑动到右边的距离」。
为什么很多人会觉得 iPhone 的体验比绝大多数的安卓手机要好,看看这个关机界面就知道原因在哪里了吧 。
四. 总结
在文章的最后,回顾一下费茨定律给我们的启示:
- 按钮做大点(W大点)更易于点击。
- 将按钮放置在离开始点较近的地方。
- 相关按钮之间距离近点(D小点)更易于点击。
- 屏幕的四角与四边是「无限可选中」位置。
- 通过费茨定律的反向使用,可以降低按钮被点击的可能。
欢迎关注微信公众号:「UXD-Cloudhub」
