IT博客汇 | R语言做符号计算

R语言做符号计算

黄湘云发表于 2016-07-08 11:48:37

本文作者：黄湘云，2011-2015年在中国矿业大学（北京）的数学与应用数学专业获得学士学位，并从2015年至今在中国矿业大学（北京）统计学专业硕士在读，主要研究方向为复杂数据分析。

引言

谈起符号计算，大家首先想到的可能就是大名鼎鼎的Maple，其次是Mathematica，但是他们都是商业软件，除了其自身昂贵的价格外，对于想知道底层，并做一些修改的极客而言，这些操作也很不可能实现。自从遇到R以后，还是果断脱离商业软件的苦海，R做符号计算固然比不上Maple，但是你真的需要Maple这样的软件去做符号计算吗？我们看看R语言的符号计算能做到什么程度。

符号计算

1.符号微分

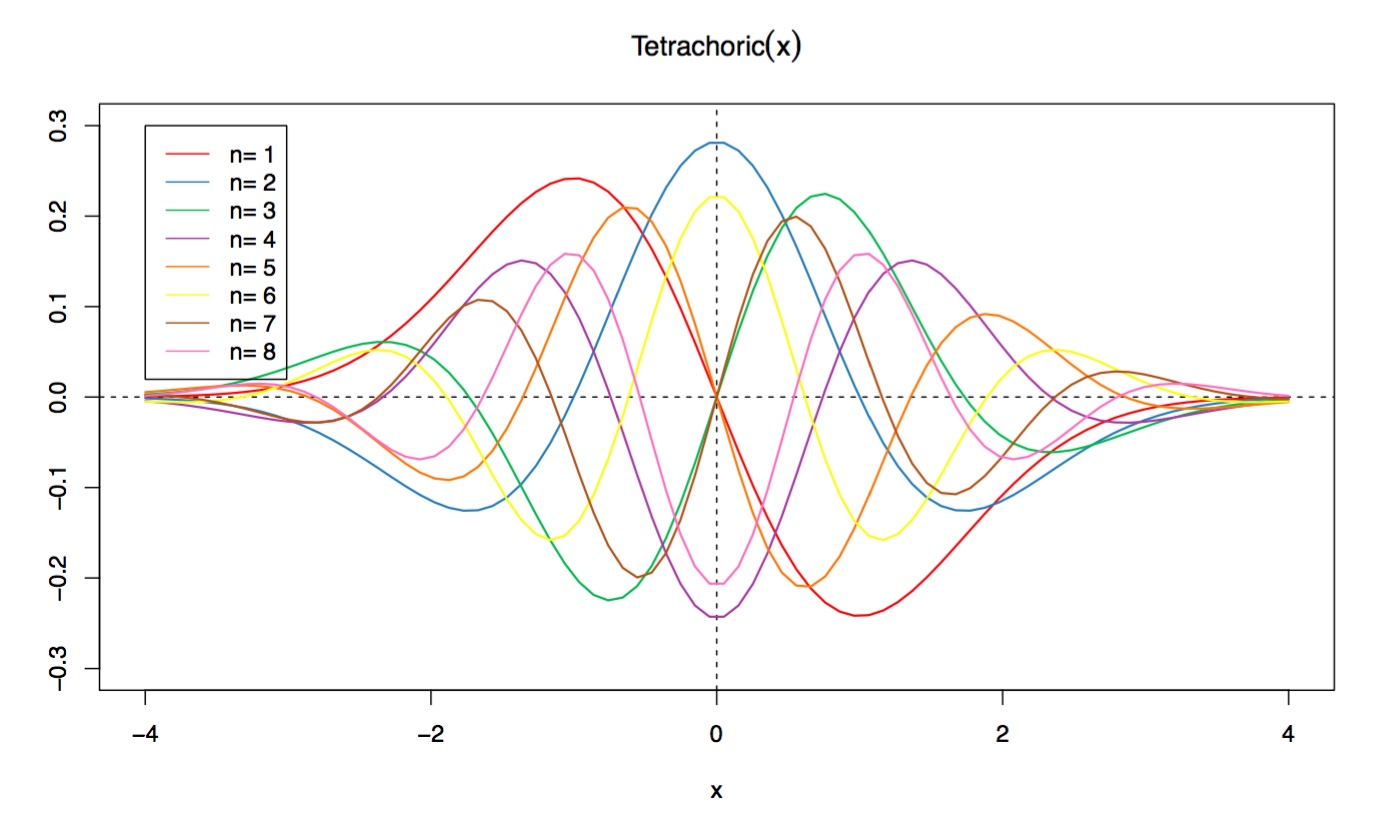
在R中能够直接用来符号计算的是表达式，下面以Tetrachoric函数为例，
$$\tau(x)=\frac{(-1)^{j-1}}{\sqrt{j !}}\phi^{(j)}(x)$$
其中
$$\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$
在R里，声明表达式对象使用expression函数

NormDensity <- expression(1/sqrt(2 * pi) * exp(-x^2/2))
class(NormDensity)
## [1] "expression"

计算一阶导数

D(NormDensity, "x")
## -(1/sqrt(2 * pi) * (exp(-x^2/2) * (2 * x/2)))
deriv(NormDensity, "x")
## expression({
##      .expr3 <- 1/sqrt(2 * pi)
##      .expr7 <- exp(-x^2/2)
##      .value <- .expr3 * .expr7
##      .grad <- array(0, c(length(.value), 1L), list(NULL,c("x")))
##      .grad[, "x"] <- -(.expr3 * (.expr7 * (2 * x/2)))
##      attr(.value, "gradient") <- .grad
##     .value
## })

deriv3(NormDensity, "x")

## expression({
##     .expr3 <- 1/sqrt(2 * pi)
##     .expr7 <- exp(-x^2/2)
##     .expr10 <- 2 * x/2
##     .expr11 <- .expr7 * .expr10
##     .value <- .expr3 * .expr7
##     .grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
##     .hessian <- array(0, c(length(.value), 1L, 1L), list(NULL, 
##     c("x"), c("x")))
##     .grad[, "x"] <- -(.expr3 * .expr11)
##     .hessian[, "x", "x"] <- -(.expr3 * (.expr7 * (2/2) - .expr11  
##     ＊.expr10))
##     attr(.value, "gradient") <- .grad
##     attr(.value, "hessian") <- .hessian
##     .value
## })

计算 n 阶导数

DD <- function(expr, name, order = 1) {
    if (order < 1)
        stop("'order' must be >= 1")
    if (order == 1)
        D(expr, name) else DD(D(expr, name), name, order - 1)
DD(NormDensity, "x", 3)
## 1/sqrt(2 * pi) * (exp(-x^2/2) * (2 * x/2) * (2/2) + ((exp(-x^2/2) * 
## (2/2)-exp(-x^2/2)*(2*x/2)*(2*x/2))*(2*x/2)+
## exp(-x^2/2) * (2 * x/2) * (2/2)))

2.表达式转函数

很多时候我们使用R目的是计算，符号计算后希望可以直接代入计算，那么只需要在deriv中指定function.arg参数为TRUE。

DFun <- deriv(NormDensity, "x", function.arg = TRUE)
DFun(1)

## [1] 0.2419707
## attr(,"gradient")
##               x
## [1,] -0.2419707


DFun(0)


## [1] 0.3989423
## attr(,"gradient")
## x 
## [1,] 0

从计算结果可以看出,deriv 不仅计算了导数值还计算了原函数在该处的函数值。我们可以作如下简单验证:

Normfun <- function(x) 1/sqrt(2 * pi) * exp(-x^2/2)
Normfun(1)

## [1] 0.2419707

Normfun(0)

## [1] 0.3989423

在讲另外一个将表达式转化为函数的方法之前,先来一个小插曲,有没有觉得之前计算 3 阶导数的结果太复杂了,说不定看到这的人,早就要吐槽了! 其实这个问题已经有高人写了 Deriv 包 [1] 来解决,请看:

DD(NormDensity, "x", 3)

## 1/sqrt(2 * pi) * (exp(-x^2/2) * (2 * x/2) * (2/2) + ((exp(-x^2/2) * 
## (2/2)-exp(-x^2/2)*(2*x/2)*(2*x/2))*(2*x/2)+
## exp(-x^2/2) * (2 * x/2) * (2/2)))


library(Deriv)
Simplify(DD(NormDensity, "x", 3))
## x * (3 - x^2) * exp(-(x^2/2))/sqrt(2 * pi)

三阶导数根本不在话下，如果想体验更高阶导数，不妨请读者动动手！
表达式转函数的关键是理解函数其实是由参数列表(args)和函数体(body)两部分构成，
以前面自编的Normfun函数为例

body(Normfun)

## 1/sqrt(2 * pi) * exp(-x^2/2)

args(Normfun)

## function (x)
## NULL

而函数体被一对花括号括住的就是表达式，查看eval函数帮助，我们可以知道eval计算的对象就是表达式。
下面来个小示例以说明此问题。

eval({x<-2;x^2})
eval(body(Normfun))
Normfun(2)

## [1] 4

eval(body(Normfun))

## [1] 0.05399097

Normfun(2)

## [1] 0.05399097

至此我们可以将表达式转化为函数，也许又有读者耐不住了，既然可以用eval函数直接计算，干嘛还要转化为函数？这个主要是写成函数比较方便，你可能需要重复计算不同的函数值，甚至放在你的算法的中间过程中……(此处省略500字，请读者自己理解)
终于又回到开篇处Tetrachoric函数，里面要计算任意阶导数，反正现在是没问题了，管他几阶，算完后化简转函数，请看：

Tetrachoric<-function(x,j){
 (-1)^(j-1)/sqrt(factorial(j))*eval(Simplify(DD(NormDensity,"x",j)))
}
Tetrachoric(2,3)

## [1] -0.04408344

有时候我们有的就是函数，这怎么计算导数呢？按道理，看完上面的过程，这已经不是什么问题啦！

Simplify(D(body(Normfun),"x"))
## -(x * exp(-(x^2/2))/sqrt(2 * pi))

作为本节的最后，献上函数图像，这个函数的作用主要是计算多元正态分布的概率，详细内容参看 [2]。

3.符号计算扩展包Ryacas

想要做更多的符号计算内容，如解方程，泰勒展开等，可以借助第三方R扩展包Ryacas[3]。

 suppressPackageStartupMessages(library(Ryacas))
 yacas("Solve(x/(1+x) == a, x)")

 ## [1] "Starting Yacas!"
 ## expression(list(x == a/(1 - a)))

 yacas(expression(Expand((1+x)^3)))

 ## expression(x^3 + 3 * x^2 + 3 * x + 1)

 yacas("OdeSolve(y''==4*y)")

 ## expression(C95 * exp(2 * x) + C99 * exp(-2 * x))

 yacas("Taylor(x,a,3) Exp(x)")

 ## expression(exp(a) + exp(a) * (x - a) + (x - a)^2 * exp(a)/2 + 
 ## (x - a)^3 * exp(a)/6)

4.符号计算在优化算法中的应用

学过运筹学或者数值分析课程的可能知道，有不少优化算法是要求导或者求梯度的，
如拟牛顿算法，最速下降法和共轭梯度法，还有求解非线性方程组的拟牛顿算法及其修正算法。
下面以求Rosenbrock函数的极小值为例：

符号微分

 fun<-expression(100*(x2-x1^2)^2+(1-x1)^2)
 D(fun,"x1")

## -(2 * (1 - x1) + 100 * (2 * (2 * x1 * (x2 - x1^2))))

 D(fun,"x2")

## 100 * (2 * (x2 - x1^2))

调用拟牛顿法求极值

 fr <- function(x) {
 x1 <- x[1]
 x2 <- x[2]
 100 * (x2 - x1 * x1)^2 + (1 - x1)^2
 }
 grr1 <- function(x) {
 x1 <- x[1]
 x2 <- x[2]
 c(-400 * x1 * (x2 - x1 * x1) - 2 * (1 - x1),
 200 * (x2 - x1 * x1))
 }
 optim(c(-1.2,1), fr, grr1, method = "BFGS")


## $par
## [1] 1 1
## 
## $value
## [1] 9.594956e-18
## 
## $counts
## function gradient 
## 110 43 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

仿照Tetrachoric函数的写法，可以简写grr函数(这个写法可以稍微避免一点复制粘贴)：

 grr2<-function(x){
 x1 <- x[1]
 x2 <- x[2]
 c(eval(D(fun,"x1")),eval(D(fun,"x2"))) # 表达式微分
 }
 optim(c(-1.2,1), fr, grr2, method = "BFGS")


## $par
## [1] 1 1
## 
## $value
## [1] 9.594956e-18
## 
## $counts
## function gradient 
## 110 43 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

如果调用numDeriv包[4]，可以再少写点代码：

 library(numDeriv)
 grr3 <- function(x) {
 grad(fr,c(x[1],x[2])) # 函数微分
 }
 optim(c(-1.2, 1), fr, grr3, method = "BFGS")

## $par
## [1] 1 1
## 
## $value
## [1] 9.595012e-18
## 
## $counts
## function gradient 
## 110 43 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

如果一定要体现符号微分的过程，就调用Deriv包：

 library(Deriv)
 fr1 <- function(x1,x2) { # 函数形式与上面不同
 100 * (x2 - x1 * x1)^2 + (1 - x1)^2
 }

grr2 <- function(x) {
 Deriv(fr1,cache.exp = FALSE)(x[1],x[2]) # 符号微分
 }
 optim(c(-1.2, 1), fr, grr2, method = "BFGS")


## $par
## [1] 1 1
## 
## $value
## [1] 9.594956e-18
## 
## $counts
## function gradient 
## 110 43 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

从上面可以看出函数(Deriv与optim)之间不兼容：Deriv与optim接受的函数形式不同，导致两个函数(fr与fr1)的参数列表的形式不一样，应能看出fr这种写法更好些。

注:

求极值和求解方程 (组) 往往有联系的,如统计中求参数的最大似然估计,有不少可以转化为求方程 (组),如 stat4 包 [5] 的 mle 函数。
目标函数可以求导,使用拟牛顿算法效果比较好,如上例中 methods 参数设置成 CG,结果就会不一样。
nlm、optim 和 nlminb 等函数都实现了带梯度的优化算法。
不过话又说回来,真实的场景大多是目标函数不能求导,一阶导数都不能求,更多细节请读者参见optim 函数帮助。
还有一些做数值优化的 R 包,如 BB 包 [6] 求解大规模非线性系统,numDeriv 包是数值微分的通用求解器,更多的内容可参见https://cran.rstudio.com/web/views/Optimization.html。
除了数值优化还有做概率优化的 R 包,如仅遗传算法就有 GA [7],gafit [8],galts [9],mcga [10], rgenoud [11],gaoptim [12],genalg [13] 等 R 包,这方面的最新成果参考文献 [14]。

R软件信息

## R version 3.1.3 (2015-03-09)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 8 x64 (build 9200)
## 
## locale:
## [1] LC_COLLATE=Chinese (Simplified)_China.936 
## [2] LC_CTYPE=Chinese (Simplified)_China.936 
## [3] LC_MONETARY=Chinese (Simplified)_China.936
## [4] LC_NUMERIC=C 
## [5] LC_TIME=Chinese (Simplified)_China.936 
## 
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base 
## 
## other attached packages:
## [1] numDeriv_2014.2-1 Ryacas_0.2-12.1 Deriv_3.7.0 knitr_1.13 
## 
## loaded via a namespace (and not attached):
## [1] evaluate_0.9 formatR_1.3 highr_0.5.1 magrittr_1.5 
## [5] RevoUtils_7.4.0 stringi_1.0-1 stringr_1.0.0 tools_3.1.3

参考文献

[1] Andrew Clausen and Serguei Sokol. Deriv: Symbolic Differentiation, 2016. R package version 3.7.0.
[2] Bernard Harris and Andrew P. Soms. The use of the tetrachoric series for evaluating multivariate normal probabilities. Journal of Multivariate Analysis, 10(2):252–267, 1980.
[3] Ryacas: R interface to the yacas computer algebra system, 2014. R package version 0.2-12.1.
[4] Paul Gilbert and Ravi Varadhan. numDeriv: Accurate Numerical Derivatives, 2015. R package version 2014.2-1.
[5] R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2015.
[6] Ravi Varadhan and Paul Gilbert. BB: An R package for solving a large system of nonlinear equations and for optimizing a high-dimensional nonlinear objective function. Journal of Statistical Software, 32(4):1–26, 2009.
[7] Luca Scrucca. GA: Genetic Algorithms, 2016. R package version 3.0.1.
[8] Telford Tendys. gafit: Genetic Algorithm for Curve Fitting, 2012. R package version 0.4.1.
[9] Mehmet Hakan Satman. galts: Genetic algorithms and C-steps based LTS (Least Trimmed Squares) estimation, 2013. R package version 1.3.
[10] Mehmet Hakan Satman. Machine coded genetic algorithms for real parameter optimization problems. Gazi University Journal of Science, 26(1):85–95, 2013.
[11] Walter R. Mebane, Jr. and Jasjeet S. Sekhon. Genetic optimization using derivatives: The rgenoud package for R. Journal of Statistical Software, 42(11):1–26, 2011.
[12] Fernando Tenorio. gaoptim: Genetic Algorithm optimization for real-based and permutation-based problems, 2013. R package version 1.1.
[13] Egon Willighagen and Michel Ballings. genalg: R Based Genetic Algorithm, 2015. R package version 0.2.0.
[14] L. Scrucca. On some extensions to GA package: hybrid optimisation, parallelisation and islands evolution. ArXiv e-prints, May 2016.
[15] Yihui Xie. knitr: A General-Purpose Package for Dynamic Report Generation in R, 2016. R package version 1.13.

敬告各位友媒，如需转载，请与统计之都小编联系（直接留言或发至邮箱：editor@cos.name ），获准转载的请在显著位置注明作者和出处（转载自：统计之都），并在文章结尾处附上统计之都二维码。

未经许可的转载以及改编者，统计之都将依法追究其法律责任。

您可能也喜欢：
也谈提高R语言的运算效率	第九届中国R语言会议（北京）纪要	标准正态分布函数的快速计算方法	第四届中国R语言会议(上海会场)通知	第三届中国R语言会议（上海会场）纪要
无觅