数学家救火法与数学竞赛
「数学家救火法」的名字来源于著名的网络段子:
一天,数学家觉得自己已受够了数学,于是他跑到消防队去宣布他想当消防员。
消防队长说:「您看上去不错,可是我得先给您一个测试。」
消防队长带数学家到消防队后院小巷,巷子里有一个货栈,一只消防栓和一卷软管。
消防队长问:「假设货栈起火,您怎么办?」
数学家回答:「我把消防栓接到软管上, 打开水龙,把火浇灭。」
消防队长说:「完全正确。最后一个问题:假设您走进小巷,而货栈没有起火,您怎么办?」
数学家疑惑地思索了半天,终于答道:「我就把货栈点着。」
消防队长大叫起来:「什么?太可怕了,您为什么要把货栈点着?」
数学家回答:「这样我就把问题化简为一个我已经解决过的问题了。」
简单地说,这一方法的精髓在于不断地将当前问题化归为更简单的问题,直到最后化为熟悉的或已知答案的问题。解代数方程的消元法,平面几何的解析和三角法、面积「消点法」,证明不等式的累次极值法等都可以看作是这一方法的特例。在这里我们的基本原则是:
在每一步对题目进行等价变换,使题目的叙述严格变短。
这里等价变换亦可看作对信息的转移和集中,即每一步我们都将题目所给的信息集中到有限的几个「变量」上,或转移到我们更熟悉或更容易处理的「变量」上(当然这里的「变量」是广义的)。应用这一原则的前提是:
我们相信化归的过程可以在有限步内结束。
什么样的题目可以在有限步内结束呢?粗略地说,大致有以下几类。
- 所有的平面几何题;
- 能用有限个自由变量,或是附加不相牵连的限制条件的变量表出的代数问题;
- 题面所给信息较为集中,指向性较为明显的组合或数论问题。
当然单纯这么说未免失之空泛,我们还是以今年集训队的两道试题为例来展示如何运用这一方法。
例 1(2017 年集训队第二次测试第 5 题)设这种题目一看就很像「能用有限个自由变量表示出来」的题目。题目说是整系数多项式的三个根,又没有限定多项式的其它性质,所以这句无非是说
,
和
都是有理数而已,这提示我们在某个时刻需要把问题转化到初等对称多项式上。当然现在还看不出来什么——尤其是看不出来初等对称多项式之间的关系——我们只知道两个根之间有某种多项式的关系而已。对这类条件,常用的办法是利用对称性,或者得到两个多项式方程来辗转相除。
设是
满足的方程,则
是
和
的公共根。但
没有一次因式故在
上不可约,所以
,因此
和
都是
的根,从而都等于
之一。这两个数不相同(否则
是有理数),同理可知其都不等于
,且
(否则
可约了),因此只能是
和
。
此时我们已经得到了足够多关于根的信息(关于三个根轮换对称的三个方程,想要得到初等对称多项式的信息的话这已经足够),下一步可以开算了,但我们不想把这三个参数都搬过来。通过标准的变换,我们可以化归为
的情形。具体地说,作线性变换
等,则我们有
等,且
满足
。这一步虽然略显平凡,但对计算是至关重要的(使题设严格变短!),而且在考场上也能起到放松心情和增加自信的作用。
现在我们得到了(看上去挺简单的)方程组
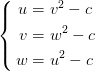
接下来可以上初等对称多项式了。当然因为方程组的形式实在简单,这个时候我们可以做一件事——用不太好翻译的英文表达来说是「play with it」,在这里就是试着对方程组进行一些变形看能得到什么。通过两两相减、相乘和约分可得,但除此之外似乎并不能看出更多的东西。于是我们回到最初的思路,注意
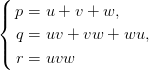
是三个完全自由的有理变量,那我们能不能导出关于它们的方程呢?当然可以。对原方程组作用初等对称多项式可得
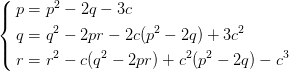 由
由还有
。
注意我们现在已经用上题目的全部条件了,所有的结论都应该能从这四个方程得出。从方程组可以看出是
的多项式,而
是
和
的多项式。因此理所当然要消去
来得到
和
的方程。从第一式可以算出
,由
可得
,代入方程组的第二式,整理得到
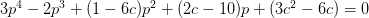 这是关于
这是关于和
的方程,但
是可以自由取值的变量,
是我们要证明满足某个条件的东西,所以正确的做法当然是从
解出
来(方程关于
恰好是二次的)。因此我们把方程写成关于
的形式
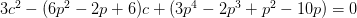 解得
解得或
(你问为什么根号能开出来?因为这个题目是对的所以能开出来)。显然
意味着
(是有理数的平方,所以也是整数的平方),而
应该是增根。怎么确认这一点呢?只要把它代入剩下的第三式,化简得到一个关于
的方程
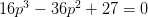 这个方程的解是
这个方程的解是和
,相应地求出
或
,通过解三次方程可以求出相应的
均为有理数,矛盾。
我们可以看到,这道题的证明虽然写得有些长,但思路是很清晰的:关键的步骤是把关于的方程化为关于
的方程。如此转化的理由是,
是三个奇奇怪怪的、满足某个三次方程的无理数,而
是三个可以自由取值的有理数。在此之后就只是普通的消元法,做每一步的时候也就能有「如果算不出来,那么要么是算错,要么是题目出错」的自信了。实际上,对有经验的选手来说第一眼就能判断出这道题肯定能做出来,只是时间问题;而数学竞赛的时间一般都是足够的。
例 2(2017 年集训队第二次测试第 6 题)设满足对任何
与
有
和
,且
和
各有内点。对实数
定义
。证明若无理数
满足
,则
或
为有理数。
第一步是从看上去乱七八糟的条件中提取(集中)有用信息。是周期的,所以本质上可以看成
的子集;有内点,说明不是性质特别坏的集合,很大可能我们只需要利用
包含一个开区间的事实。关于原点对称看不出有什么用,暂且放置。现在
无非是说
的小数部分属于
,而这自然取决于
在
上的分布。这个指向是如此明显,以至于我们不得不猜测这道题十有八九是个套路题——而且多数情况下确实是——即便不是,知道为什么不是也能使你更接近出题人的意图。
题目要求,说明
和
有一定相关性(一个属于
当且仅当另一个也属于
),因此我们首先证明
在
上线性相关;若不然,则
在
一致分布(由 Weyl 判别法可知;关于 Weyl 判别法的证明可以参见这篇笔记的第 2 节),所以必存在
使得
属于包含于
的区间,且
属于包含于
的区间,不可能。现在我们可以假设
,其中
是有理数,且
。如果
结论已经成立;如果
,注意到
,我们可以进一步简化,假定
(否则只需考虑
)。
现在在
上线性相关了;考虑特例,不妨假设
。那么我们知道
,因此题目条件等价于「如果
,则
」。如果令
,那么这句话相当于(尽管不是完全等价,因为
并不能取遍所有实数而只能取遍一个可数集)在说「如果
,则
」。
注意这已经和完全没有关系了,而仅仅是一个关于满足上述条件的集合
是否存在的问题。化简到这一步题目就并不困难了;实际上若
,由归纳法容易证明
对每个正整数
成立。由已知
包含一个开区间,所以
能够(几乎)包含任意长的区间,因而
能够(几乎)包含整个
,这便与
有内点相矛盾了。这里的关键是
,所以每步迭代所得到的区间长度越来越大,最终将能够得到矛盾。易知以上的讨论在
都为整数时可行,剩下的只是将其严格化并推广到
为有理数的情形了。
设,其中
;又设
是正整数且
,
。取充分大的正整数
(待定),及正整数
(待定),使得
,并定义
以及
。易知对每个
有
,因此我们有
。于是,若
,则必有
。若还有
,则
,故
。
综上我们得到:若,且
,则必有
。现在设
,其中
;容易证明存在
使得当
时必有
。事实上,当
充分大时
包含一个长为
的区间,因此必包含某个
,其中
为正整数。再取
即可。最后我们只需证明存在正整数
使得
以及
即可得到矛盾。而这是简单的;只需取
,其中
为正整数,且使得
即可。
好一道美妙的数学分析习题呀……我可能看到了一道假的集训队考题(笑)。不过思路依然是清晰的:从初始的小区间不断迭代到更大的区间上,直到占满整个而得出矛盾。而我们之所以能看出这个迭代过程,关键是在导出
线性相关后,把问题转化为一个仅与
相关的问题,从而形式上大大降低了题目的复杂度,也使继续下去的路径变得较为明朗。
有一点我们必须承认,数学家救火法并不适用于那些毫无套路,需要真正的「灵光一闪」的题目。不过若是对毫无套路的题目,又如何能去写所谓的经验总结呢?好在大部分的数学竞赛题依然是有套路的;而即使是在最需要灵光一闪的数学研究中,将大问题分解为若干个小问题,以及将当前问题转化为已解决问题的能力依然是至关重要的——事实上,灵感的火花有时就隐藏在这不经意的化归之中。
愿蠢萌的数学家和竞赛选手们,今天也能在消防员的道路上执着前行。
来源:知乎 www.zhihu.com
作者:Yu Deng
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载