大语言模型的涌现能力:现象与解释
注1:本文整理自我在今年3 月 11 日 “中国人工智能学会”主办的「ChatGPT 及大模型专题研讨会」上《大型语言模型的涌现能力:现象与解释》的现场分享,介绍了大语言模型中的涌现现象,以及关于涌现能力背后原因的相关猜想。感谢CSDN帮助整理的文字稿。
注2:另,有人问了,既然很多自然现象也体现出涌现能力,那么大语言模型的涌现现象需要解释吗?我个人认为是需要的。毕竟,说大语言模型的某个特殊现象属于“涌现现象”,也是被个别研究提出来,未有确切证明或证据,是否它和自然现象中出现的涌现现象内在机制是类似或一样的,其实可以存疑。而且我认为大模型的这个现象,背后应该有些我们可以理解的原因。如果我们不追求现象背后的解释,仅仅把目前解释不了的现象统一归类为涌现或者其它什么概念,就此了之。那么,其实我们也可以把大模型的目前理解不了的很多现象,统一归类为这是一种“神迹”,那世界上很多事情就简单多了。另另,用Grokking解释涌现现象,尽管我把它称为”用玄学解释玄学“,但是觉得还是值得深入探索的方向,也许可以把上面的说法,优化为”用含玄量较低的玄学解释另外一个含玄量较高的玄学“。
注3:如果仔细分析的话,大语言模型的这个所谓“涌现现象”,如果仅仅把现象归因于模型规模,目前看大概率是把问题简化了,很有可能影响因素是多样化的。如果让我归纳的话,某个任务,大语言模型是否会出现“涌现现象”这个变量 ,很可能是以下多因素影响的某个未知函数:
而关于此,需要进一步更深入的研究与解释。
什么是大模型的涌现能力
复杂系统学科里已经对涌现现象做过很久的相关研究。那么,什么是“涌现现象”?当一个复杂系统由很多微小个体构成,这些微小个体凑到一起,相互作用,当数量足够多时,在宏观层面上展现出微观个体无法解释的特殊现象,就可以称之为“涌现现象”。

在日常生活中也有一些涌现现象,比如雪花的形成、堵车、动物迁徙、涡流形成等。这里以雪花为例来解释:雪花的构成是水分子,水分子很小,但是大量的水分子如果在外界温度条件变化的前提下相互作用,在宏观层面就会形成一个很规律、很对称、很美丽的雪花。
那么问题是:超级大模型会不会出现涌现现象?显然我们很多人都知道答案,答案是会的。
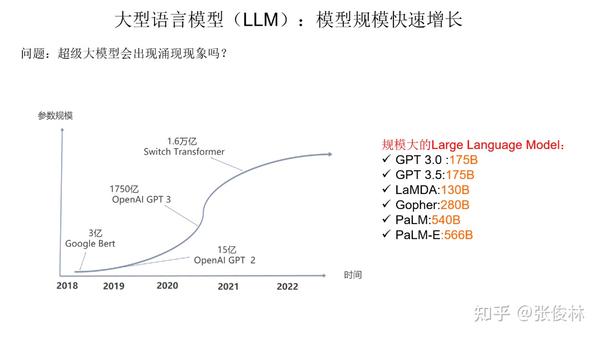
我们先来看下大语言模型的规模增长情况。如果归纳下大语言模型在近两年里最大的技术进展,很有可能就是模型规模的快速增长。如今,大规模模型一般超过 100B,即千亿参数。如 Google 发布的多模态具身视觉语言模型 PaLM-E,由540B 的 PaLM 文本模型和 22B 的 VIT图像模型构成,两者集成处理多模态信息,所以它的总模型规模是 566B。
大语言模型规模不断增长时,对下游任务有什么影响?对于不同类型的任务,有三种不同的表现:
第一类任务表现出伸缩法则:这类任务一般是知识密集型任务。随着模型规模的不断增长,任务效果也持续增长,说明这类任务对大模型中知识蕴涵的数量要求较高。

第二类任务表现出涌现能力:这类任务一般是由多步骤构成的复杂任务。只有当模型规模大到一定程度时,效果才会急剧增长,在模型规模小于某个临界值之前,模型基本不具备任务解决能力。这就是典型的涌现能力的体现。这类任务呈现出一种共性:大多数是由多步骤构成的复杂任务。
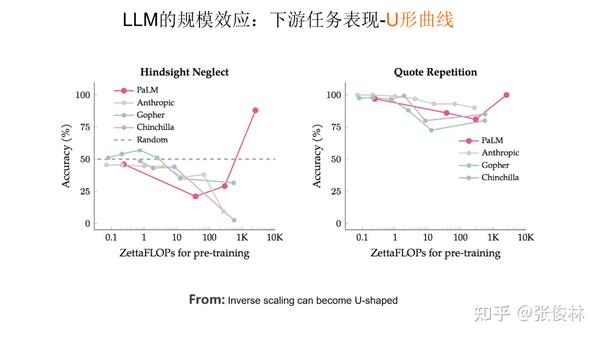
第三类任务数量较少,随着模型规模增长,任务效果体现出一个U 形曲线。如上图所示,随着模型规模增长,刚开始模型效果会呈下降趋势,但当模型规模足够大时,效果反而会提升。如果对这类任务使用 思维链CoT技术,这些任务的表现就会转化成伸缩法则,效果也会随着模型规模增长而持续上升。
因此,模型规模增长是必然趋势,当推进大模型规模不断增长的时候,涌现能力的出现会让任务的效果更加出色。
LLM 表现出的涌现现象

目前有两大类被认为具有涌现能力的任务,第一类是 In Context Learning(“Few-Shot Prompt”),用户给出几个例子,大模型不需要调整模型参数,就能够处理好任务(参考上图给出的情感计算的例子)。

如上图展示,利用In Context Learning,已经发现在各种类型的下游任务中,大语言模型都出现了涌现现象,体现在在模型规模不够大的时候,各种任务都处理不好,但是当跨过某个模型大小临界值的时候,大模型就突然能比较好地处理这些任务。
第二类具备涌现现象的技术是思维链( CoT)。CoT本质上是一种特殊的few shot prompt,就是说对于某个复杂的比如推理问题,用户把一步一步的推导过程写出来,并提供给大语言模型(如下图蓝色文字内容所示),这样大语言模型就能做一些相对复杂的推理任务。


从上图可以看出,无论是数学问题、符号推理问题,CoT 都具备涌现能力。
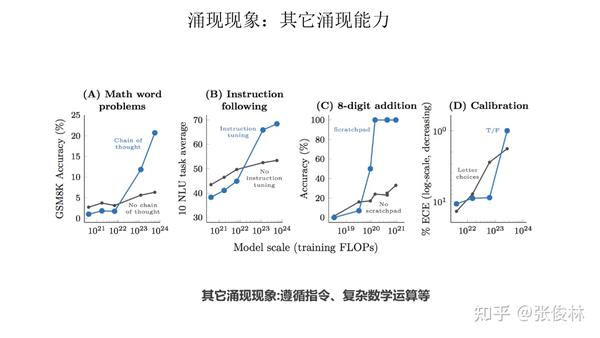
除此之外,其他任务也有涌现能力,如上图所示的数学多位数加法、命令理解等。
LLM 模型规模和涌现能力的关系
可以看出,涌现能力和模型的规模大小有一定的关联关系 ,那么,我们的问题是,具体而言,两者是怎样的关系呢?
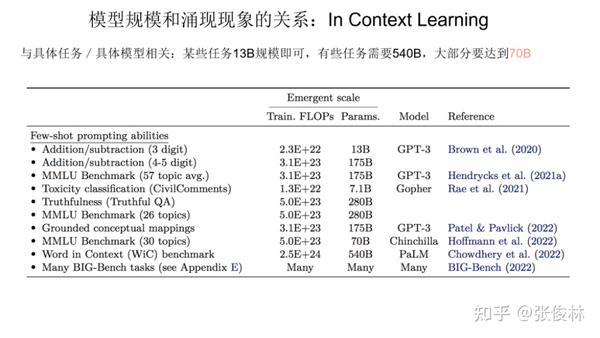
我们分头来看,先看下In Context Learning 的涌现能力和模型规模的关系。上图展示了对于不同类型的具体任务, In Context Learning 的涌现能力和模型规模的对照关系。
从图中数据可以看出,我们很难给出一个唯一的模型大小数值。不同类型的任务,在In Context Learning方面,模型多大才具备涌现能力,这跟具体的任务有一定的绑定关系。例如:图表第一行的3位数加法任务,模型只要达到 13B(130亿参数),就可以具备涌现能力,但是对倒数第二行的 Word in Context Benchmark任务而言,目前证明,只有540B 大小的模型才可以做到这点。我们只能说,就In Context Learning而言,如果模型达到 100B, 大多数任务可以具备涌现能力。

对于CoT来说,结论也是类似的,就是说要想出现涌现能力,模型规模大小和具体任务有一定的绑定关系。
把模型做小会影响 LLM 的涌现能力吗?
因为对很多任务来说,只有模型规模做到比较大,才能具备涌现能力,所以我个人比较关心下列问题:我们能不能把模型做小?把模型做小是否会影响到LLM的涌现能力?这是个很有趣的问题。我们这里拿两个小模型代表来探讨这个问题。
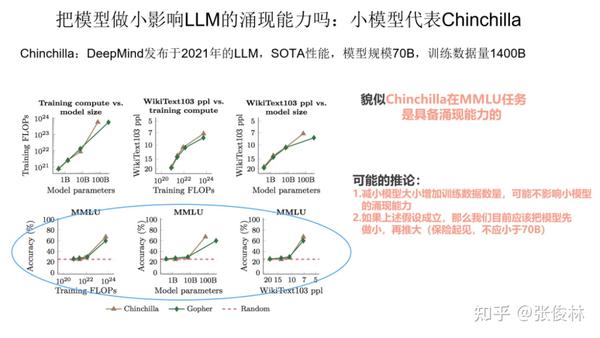
第一个小模型代表,是 DeepMind 2021年发表的模型 Chinchilla,这个模型目前做各种任务的效果,和 540B大小的PaLM 基本相当。Chinchilla的思路是给更多的数据,但是把模型规模做小。具体而言,它对标的是Gopher模型,Chinchilla模型大小只有 70B,是Gopher的四分之一,但是付出的代价是训练数据总量,是Gopher的四倍,所以基本思路是通过放大训练数据量,来缩小模型规模。
我们把Chinchilla规模做小了,问题是它还具备涌现能力吗?从上图给出的数据可以看出,起码我们可以说, Chinchilla 在自然语言处理的综合任务 MMLU 上是具备涌现能力的。如果小模型也能具备涌现能力,那么这其实侧面反映了一个问题:对于类似 GPT3 这样的模型而言,很可能它175B 这么多的模型参数,并没有被充分利用,因此,我们在以后训练模型的时候,可以考虑先增加训练数据,降低模型参数量,把模型做小,先把模型参数利用充分,在这个基础上,再继续增加数据,并推大模型规模。也即是说,目前看,我们先把模型做小,再把模型做大,看上去是可行的。
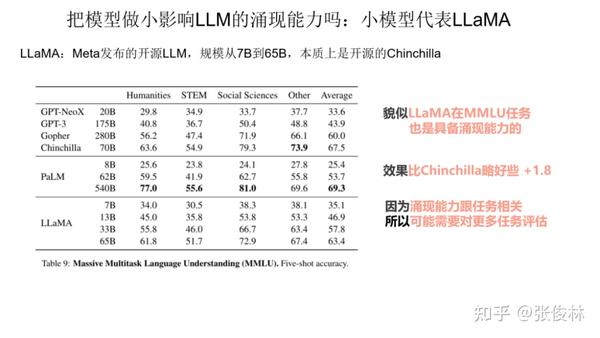
第二个小模型代表是 Meta 发布的开源模型 LLaMA,它的做法其实很好理解,本质上就是开源的 Chinchilla,它的思路是完全遵照 Chinchilla 来做的,就是说增加训练数据,但是把模型规模做小。那么LLaMA是否具备涌现能力呢?从上图表格数据可以看出, 虽然LLaMA 在MMLU这个任务上比 Chinchilla 稍差一些,但是效果也不错。这说明LLaMA在MMLU上基本也是具备涌现能力的。
其实,有个工作目前还没有看到有人做,但是这个工作是很有价值的,就是充分测试当模型变得足够小(比如10B-50B规模)以后,各种任务的涌现能力是否还具备?这是个很有价值的事情,因为如果我们的结论是即使把模型规模做小,各种任务的涌现能力可以保持,那么我们就可以放心地先追求把模型做小。
模型训练中的顿悟现象
这里介绍一个比较新的研究方向,顿悟现象,英文叫 “Grokking”。 在这里介绍模型训练过程中的顿悟,目的是希望建立起它和大模型涌现能力之间的联系,我在本文后面会尝试用顿悟现象来解释大模型的涌现能力。
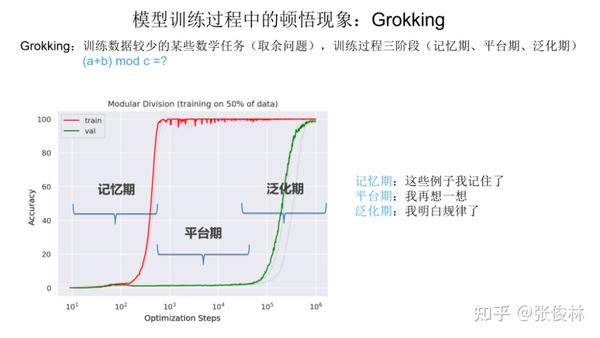
我们首先解释下什么是顿悟现象。如上图所示,对于一个训练数据较少的数学任务(通常是数字求和取余数的问题),研究人员发现一种新奇的现象。比如我们将数据集切成两块,50% 数据作为训练集(图中红线展示了随着训练过程往后走,任务指标的变化情况),50% 的数据作为验证集(图中绿线的走势展示了训练动态)。在学习数字求和取余这个任务时,它的训练动态会经历三个阶段:
- 第一个阶段是记忆期:红线对应的训练数据指标突然走高,代表模型记住了50%的训练数据的结果,而绿线对应的验证集指标接近0,说明模型完全没有泛化能力,就是说没有学会这个任务的规律。所以这个阶段模型只是在单纯地记忆训练数据。
- 第二个阶段是平台期:这个阶段是记忆期的延续,体现为验证集合效果仍然很差,说明模型仍然没有学会规律。
- 第三个阶段是泛化期:这个阶段验证集合效果突然变好,这说明突然之间,模型学会了任务里的规律,也就是我们说的,出现了顿悟现象,突然就学明白了。
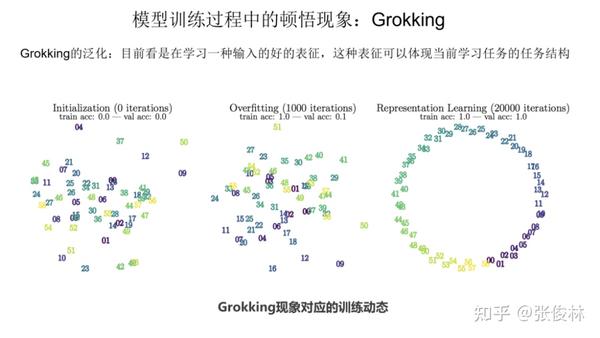
后续研究表明:Grokking 本质上是在学习输入数字的一个好的表征。如图所示,可以看到由初始化向记忆期再到顿悟现象出现的过程,数字的表征逐步开始体现当前学习任务的任务结构。

那么 ,我们能用Grokking 来解释大模型的涌现现象吗?目前,有部分研究暗示两者实际是存在某些关联的,但尚未有研究明确地指出两者之间的关系。两者从走势曲线看是非常接近的,但是有很大区别,因为Grokking描述的是模型训练动态中的表现,而涌现表达的是模型规模变化时的任务表现,虽然走势相近,但两者不是一回事。我认为,要想用Grokking解释涌现现象,核心是要解释清楚下列问题:为什么规模小的语言模型不会出现 Grokking ?这是个很关键的问题。因为如果规模小以及规模大的语言模型都会出现Grokking,那么说明Grokking和模型规模无关,也就不可能用来解释大模型的涌现现象。本文后面,我会给出一个自己的猜想,来建立两者之间的联系。
LLM 涌现能力的可能原因
为什么随着模型增大会出现涌现现象?这里给出三种猜想。前两种是现有文献提出的,第三个是我试图采用Grokking来解释涌现现象的猜想。

猜想一:任务的评价指标不够平滑
一种猜想是因为很多任务的评价指标不够平滑,导致我们现在看到的涌现现象。关于这一点,我们拿 Emoji_movie 任务来给出解释。Emoji_movie任务是说输入 Emoji图像,要求 LLM 给出完全正确的电影名称,只有一字不错才算正确,错一个单词都算错。 如上图所示,输入的Emoji是一个女孩的笑脸,后面跟着三张鱼类的图片,您可以猜猜这是什么电影。下面左侧的 2m代表 模型参数规模是 200 万参数,以及对应模型给出的回答。可以看出,随着模型规模不断增大至 128B 时,LLM才能完全猜对电影名称,但是在模型到了125m和4b的时候,其实模型已经慢慢开始接近正确答案了。
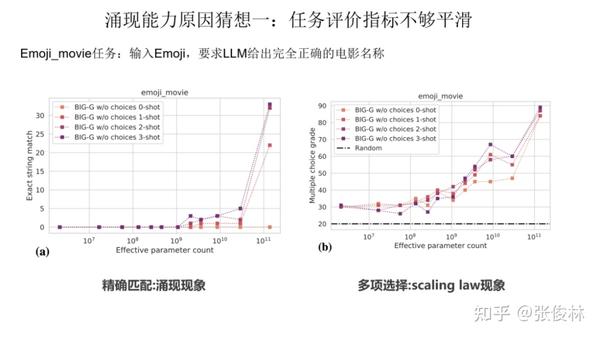
如果评价指标要求很严格,要求一字不错才算对,那么Emoji_movie任务我们就会看到涌现现象的出现,如上图图左所示。但是,如果我们把问题形式换成多选题,就是给出几个候选答案,让LLM选,那么随着模型不断增大,任务效果在持续稳定变好,但涌现现象消失,如上图图右所示。这说明评价指标不够平滑,起码是一部分任务看到涌现现象的原因。
猜想二:复杂任务 vs 子任务
开始的时候我们提到过,展现出涌现现象的任务有一个共性,就是任务往往是由多个子任务构成的复杂任务。也就是说,最终任务过于复杂,如果仔细分析,可以看出它由多个子任务构成,这时候,子任务效果往往随着模型增大,符合 Scaling Law,而最终任务则体现为涌现现象。这个其实好理解,比如我们假设某个任务 T 有 5 个子任务 Sub-T 构成,每个 sub-T 随着模型增长,指标从 40% 提升到 60%,但是最终任务的指标只从 1.1% 提升到了 7%,也就是说宏观上看到了涌现现象,但是子任务效果其实是平滑增长的。
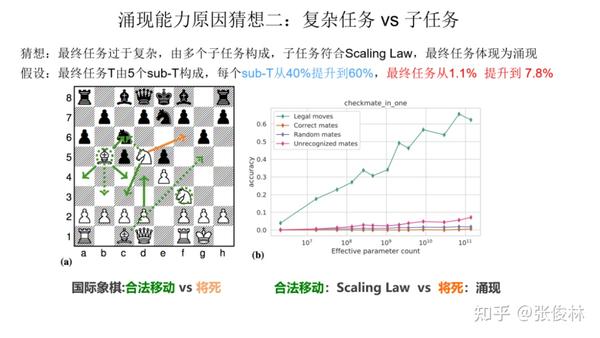
我们拿下国际象棋任务来作为例子,如上图所示,让语言模型预测下一步,最终评价指标是只有“将”死才算赢。如果按“将死”评估(红线),发现随着模型增大,模型在缓慢上升,符合涌现的表现。若评估LLM合法移动(绿线),而在合法的移动步骤里进行正确选择才够最后“将死”是个子任务,所以其实这是比将死简单的一个子任务。我们看合法移动随着模型规模,效果持续上升。此时,我们是看不到涌现现象的。

这里可以给出一个例证,如上图所示,对于CoT 任务,谷歌用 62B 和 540B 模型对LLM做错的例子进行了错误分析。对于62B做错、而540B做对的例子分析,可以看出,最多的一类错误来自于单步推理错误,这其实也能侧面说明复杂任务和子任务的关系。
猜想三:用 Grokking 来解释涌现
这里介绍我设想的如何用Grokking来解释涌现现象的一种猜想,在建立两者之间关系前,我们先来看两个已知的事实,然后在事实基础上作出推论。
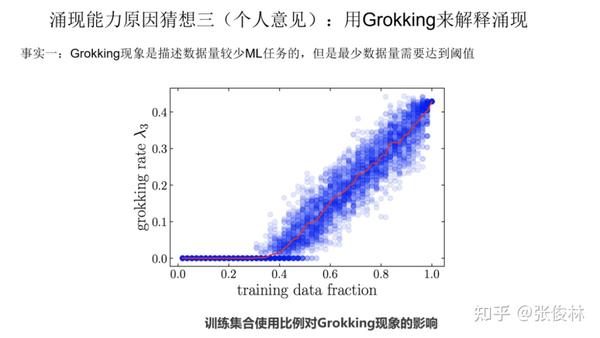
首先,第一个事实是 Grokking 现象是描述训练数据量较少的 ML 任务的,但是任务最小训练数据量必须达到一定的量,才会出现 Grokking 现象。这里有两点,一个是本身训练数据量少,另外是最小数据量要达到临界值。只有同时满足上面两个条件,才有可能出现Grokking现象。上图的意思是:当我们只拿40%及以下比例的数据来训练模型的时候,我们看不到Grokking现象,只有记忆没有泛化,只有最小训练数据比例超过40%,才会出现模型的顿悟。这是一个已被验证的事实。
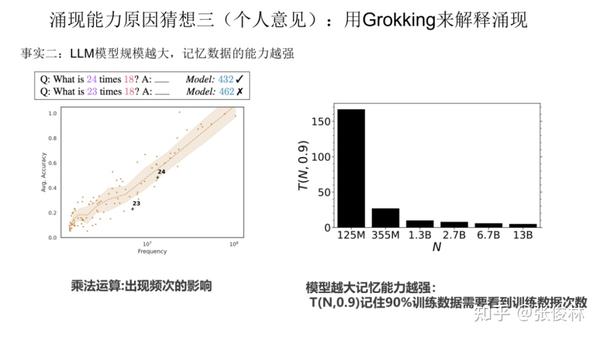
第二个事实是 LLM 模型规模越大,记忆数据的能力越强。关于这点目前有很多研究已经可以证明,如果简单理解的话,可以理解为:对于某个任务T,假设预训练数据里包含与任务T相关的训练数据量有100条,那么大模型可以记住其中的70条,而小模型可能只能记住30条。虽不精确,但大概是这个意思。

在上面的两个事实基础上,我们试图来用Grokking解释大模型的涌现现象。首先我们给出一个简单的解释,这个解释只需要利用第一个事实即可,就是说,任务的最少训练数据量需要达到临界值,才会出现Grokking。在这个事实下,对于某个任务T,尽管我们看到的预训练数据总量是巨大的,但是与T相关的训练数据其实数量很少。当我们推大模型规模的时候,往往会伴随着增加预训练数据的数据量操作,这样,当模型规模达到某个点的时候,与任务T相关的数据量,突然就达到了最小要求临界点,于是我们就看到了这个任务产生了Grokking现象。在语言模型的宏观角度,看起来就是模型达到了某个规模,突然任务T效果就开始变好,而模型规模较小的时候,因为没有达到临界值,所以一直没有Grokking现象,看起来就是语言模型没有这个能力。这是一种可以从Grokking角度解释大模型涌现现象的可能。

上面这个猜想其实有个约束条件,因为我们有个假设,说随着模型规模增大,训练数据量也在增大。如果这个假设不存在,也就是说,随着模型规模增大,我们固定住训练数据量不变。那么,这种情况下,怎么能用Grokking解释涌现现象呢?此时如果我们同时利用事实1和事实2,也可以给出一个解释。更具体来说,我们假设在预训练数据中,某个任务T有 100 个训练数据,当模型规模小的时可能只记得 30 个,达不到Grokking现象的临界点,而当模型规模推大时,因为模型记忆能力增强,可能就能记住其中的50个,这意味着它可能超过了Grokking的临界点,于是会出现 Grokking 里面的泛化现象。如果从这个角度看,其实我们也可以从Grokking角度来解释为何只有大模型才会具备涌现现象。
来源:知乎 www.zhihu.com
作者:张俊林
【知乎日报】千万用户的选择,做朋友圈里的新鲜事分享大牛。 点击下载