发表于
2025-05-24 04:19:41
趣题:正方形棋盘的双向分割
下面这个问题来自 2015 年俄罗斯数学竞赛。一个正方形棋盘能沿着网格线分成 n 个大小形状相同的小块,每块都有 k 个小格。证明:这个正方形棋盘一定能沿着网格线分成 k 个大小形状相同的小块,每块都有 n 个小格。假设正方形棋盘的边长为 s ,则 nk = s2,即 n/s = s/k。假设它们约分后都等于 p/q。如果第一个分数约掉了 a 得到 p/q,这说明 ap = n,aq = s;如果第二个分数约掉了 b 得到 p/q,这说明 bp = s,bq = k。把正方形棋盘分成 q 行,每行 a 个小方格;把正方形棋盘分成 b 列,每列 p 个小方格。这就得到了 bq = k 个大小形状相同的小长方形,每个小长方形里都有 ap = n 个小格。
...继续阅读
(15)
发表于
2025-05-17 01:29:23
趣题:房间里有几个说假话的人
下面的题目来自 2025 年孟加拉国数学竞赛的第 1 题有一个小岛,上面的居民要么只说真话,要么只说假话。某个房间里有几位岛民,其中三位岛民分别说了下面三句话。这个房间里的人数不超过 3 人。所有人都是说假话的人。这个房间里的人数不超过 4 人。不是所有人都是说假话的人。这个房间里的人数为 5 人。至少有 3 个人是说假话的人。房间里有几个人?其中有几个说假话的人?答案:房间里有 4 个人。其中有 2 个说假话的人。如果第一个人说的是真话,这就和他说的后半句话矛盾。所以第一个人说的是假话。这说明房间里的人数大于 3 人,并且有的人说真话。如果第二个人说的是假话,他说的后半句话就和事实矛盾。所以第二个人说的是真话。这说明房间里的人数小于等于 4 人。于是房间里的人数恰为 4 人。所以第三个人说的是假话。这说明房间里说假话的人数小于 3 人。但是我们已经知道了第一个人和第三个人是说假话的人,所以房间里说假话的人数恰为 2 人。
...继续阅读
(16)
发表于
2025-05-15 01:17:31
一个扑克牌小魔术及其原理的无字证明
以下面的结论为基础,可以创作很多扑克牌小魔术。设正整数 n、k 满足 n ≤ 2k ≤ 2n。将 n 张牌叠成一摞,然后用发牌的方式把上面 k 张牌发成一摞,再把剩余的牌叠上去。整个过程再重复三次,则这 n 张牌会变回成原顺序。证明:
...继续阅读
(15)
发表于
2023-02-13 01:06:20
Nim 游戏的若干变种
今年我为北京世纪坛的数学益智游戏展贡献了不少内容。我打算在这里记录一些自己的创作、发现、收获和心得。这是该系列的第三篇。今年的数学益智游戏展有一个特色,就是到访者可以购买一个小册子,这可以为自己的参展体验加分。我们内部把它叫作“任务单”。任务单里有很多任务,对应了展会中的各种项目。完成任务可以获得印章,赢取奖励。为了增加任务单的附加价值,任务单上还附赠了很多简单展品的高级玩法说明。这里举一个有趣的例子。展会现场有很多冰糕棍,可以用来做冰糕棍炸弹。任务单上给出了冰糕棍的另一种玩法——Nim 游戏。将冰糕棍从左到右摆成若干堆。两人轮流从其中一堆冰糕棍中取走任意数量的冰糕棍(可以全部取走,但不能不取)。取走最后一根冰糕棍的玩家获胜。考虑到任务单的读者可能已经熟悉 Nim 游戏了,因此为了让所有人都能有新的收获,我补充了一些不太常见的 Nim 游戏变种。我一共准备了 10 条补充规则。游戏开始前,双方可以任选其中一条来玩。每次只能从最左端或者最右端的那一堆中取冰糕棍。每次只能从冰糕棍数最多的那一堆中取冰糕棍(如果冰糕棍数最多的堆出现了并列的情况,任选其中一堆即可)。每次只能从冰糕棍数最少的那一堆中取冰糕棍(如果冰糕棍数最少的堆出现了并列的情况,任选其中一堆即可)。第一个人可以从任意一堆中取冰糕棍,今后每个人只能从和刚才不同的堆中取冰糕棍。第一个人可以从任意一堆中取冰糕棍,今后每个人只能从和
...继续阅读
(17)
发表于
2023-02-13 01:06:20
Nim 游戏的若干变种
今年我为北京世纪坛的数学益智游戏展贡献了不少内容。我打算在这里记录一些自己的创作、发现、收获和心得。这是该系列的第三篇。今年的数学益智游戏展有一个特色,就是到访者可以购买一个小册子,这可以为自己的参展体验加分。我们内部把它叫作“任务单”。任务单里有很多任务,对应了展会中的各种项目。完成任务可以获得印章,赢取奖励。为了增加任务单的附加价值,任务单上还附赠了很多简单展品的高级玩法说明。这里举一个有趣的例子。展会现场有很多冰糕棍,可以用来做冰糕棍炸弹。任务单上给出了冰糕棍的另一种玩法——Nim 游戏。将冰糕棍从左到右摆成若干堆。两人轮流从其中一堆冰糕棍中取走任意数量的冰糕棍(可以全部取走,但不能不取)。取走最后一根冰糕棍的玩家获胜。考虑到任务单的读者可能已经熟悉 Nim 游戏了,因此为了让所有人都能有新的收获,我补充了一些不太常见的 Nim 游戏变种。我一共准备了 10 条补充规则。游戏开始前,双方可以任选其中一条来玩。每次只能从最左端或者最右端的那一堆中取冰糕棍。每次只能从冰糕棍数最多的那一堆中取冰糕棍(如果冰糕棍数最多的堆出现了并列的情况,任选其中一堆即可)。每次只能从冰糕棍数最少的那一堆中取冰糕棍(如果冰糕棍数最少的堆出现了并列的情况,任选其中一堆即可)。第一个人可以从任意一堆中取冰糕棍,今后每个人只能从和刚才不同的堆中取冰糕棍。第一个人可以从任意一堆中取冰糕棍,今后每个人只能从和
...继续阅读
(10)
发表于
2023-02-06 10:13:17
怎样给孩子设计一些好的谜题
发表于
2023-02-06 10:13:17
怎样给孩子设计一些好的谜题
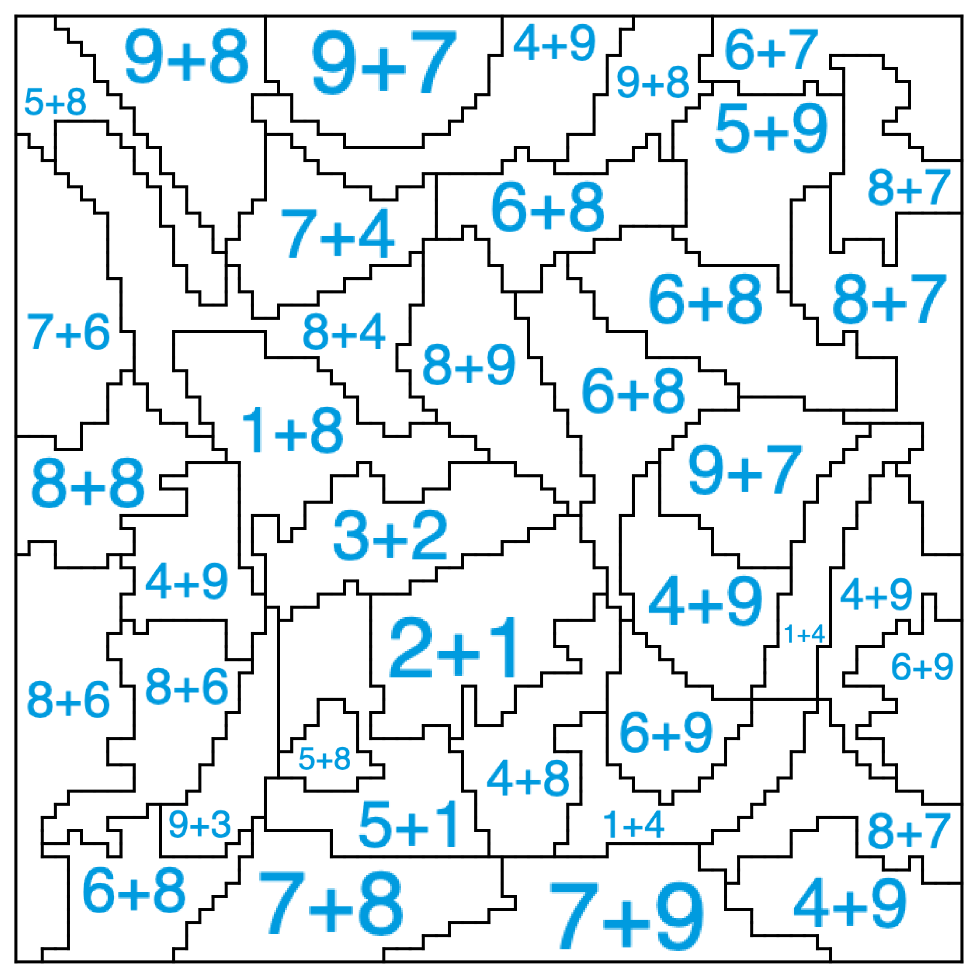
今年我为北京世纪坛的数学益智游戏展贡献了不少内容。我打算在这里记录一些自己的创作、发现、收获和心得。顺便结合一下这几年的经历。这是该系列的第二篇。两个孩子经常早晨 6 点就醒了,然后频频闯进我们卧室,给我们看他们用纸折的袜子,用乐高搭的袋熊,用水彩笔画的比萨,搞得我和孩子他妈没法睡觉。去年 5 月份左右,孩子他妈想了一个办法:在我们卧室门口放了一个纸糊的小信箱,让孩子把要给我们看的东西放信箱里。现在早晨果然能多睡一会儿了。几天后,孩子闹着说,他们想让自己的屋子门口也有个信箱。孩子他妈真又做了一个弄上去了。在信箱里放啥呢?于是我决定每天给孩子设计一些印在纸上的小活动,比如照图示折纸呀,比如看图编对话呀,比如自制两可图呀,等等。当然,还有很多我专门设计的谜题。究竟怎样的谜题才算好的谜题,这话题就太大了。不过今天我想分享一些给孩子设计谜题时我喜欢注意的三点:找到答案会自动带来奖励。孩子会因为成就感和外部奖励以外的原因进行解谜。答案具备自我检查机制。即使孩子把答案做错了,他自己也能意识到。解谜流程是非线性的。解谜的线索往往有冗余。解谜过程可以是多线并行的,不会因为卡在某一步而死掉。学校考试里的多数单选题不满足任何一条。利用电子游戏这个媒介,这几条很容易全都实现。解开谜题后可以解锁新的内容,这就实现了第 1 条。电脑可以自动判断答案的正误,这就实现了第 2 条。第 3 条也很容易做到。比如,
...继续阅读
(15)
发表于
2023-01-29 00:34:41
复原小时候见过的数学魔术
发表于
2023-01-29 00:34:41
复原小时候见过的数学魔术
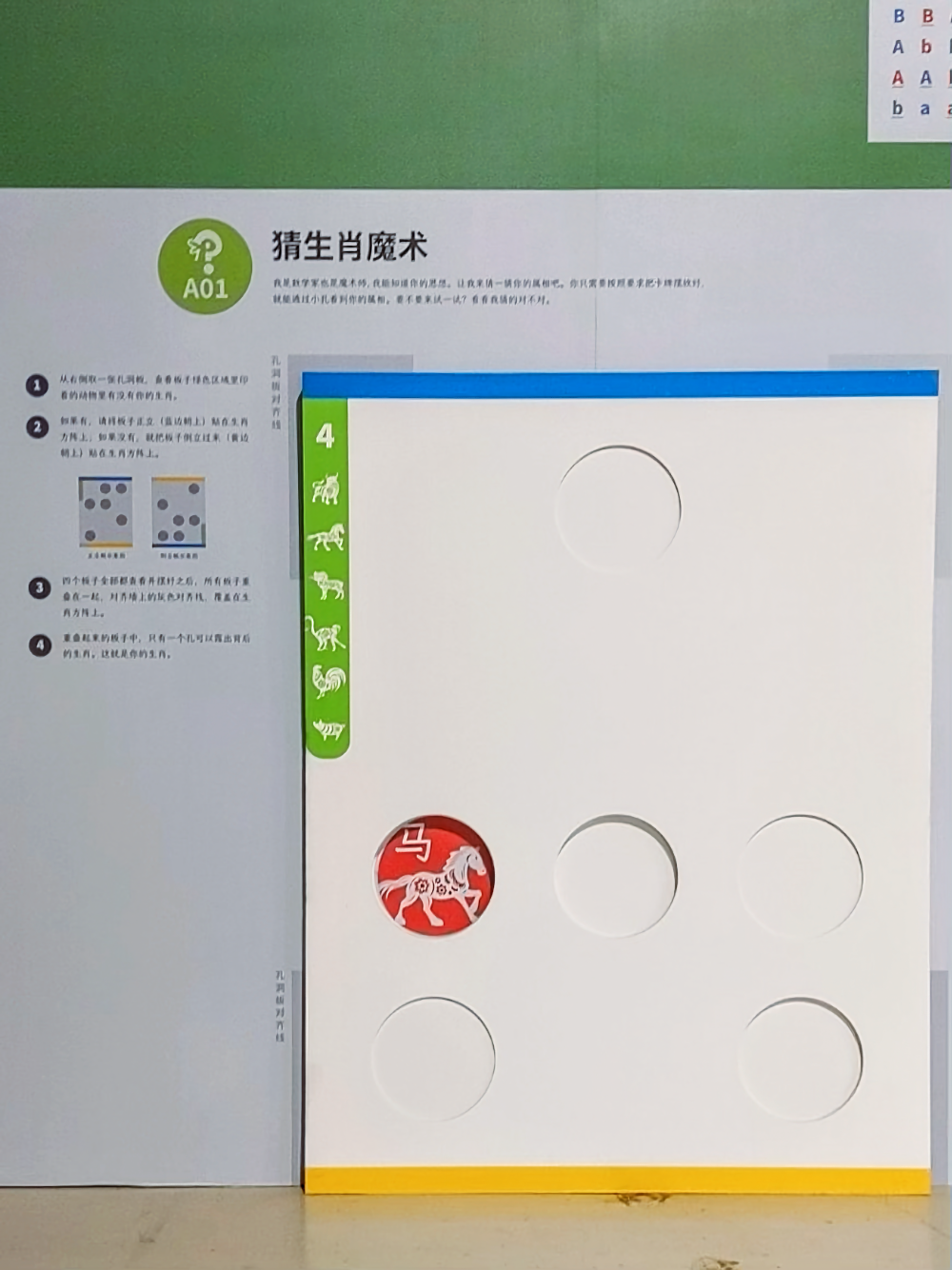
今年我为北京世纪坛的数学益智游戏展贡献了不少内容。我打算在这里记录一些自己的创作、发现、收获和心得。顺便结合一下这几年的经历。这是该系列的第一篇。有一个经典的数学小魔术。把 0 到 63 之间的数写在 6 张纸条上,其中第 1 张纸条上写着二进制表达中右起第 1 位数字为 1 的数,第 2 张纸条上写着二进制表达中右起第 2 位数字为 1 的数,第 3 张纸条上写着二进制表达中右起第 3 位数字为 1 的数,等等。给人展示 6 张纸条,问他“你的年龄出现在了哪些纸条里”。对方给出的答案就相当于告诉了你,他的年龄的二进制表达中各个地方是 0 还是 1。你就能报出他的年龄了。今年的展会有一个主题就是过年。我们打算设计一个类似的小魔术,只不过把年龄改成生肖。由于生肖有 12 个,因此 4 张纸条就可以做到这一点。为了让魔术能自动呈现出来,不需要工作人员表演,我们想到一个方法。把 4 张纸条换成 4 对带孔的板子,不妨把这些板子记作 1A、1B、2A、2B、3A、3B、4A、4B。墙上印有和板子一样大的海报。海报上印有十二生肖,排成一个 3 × 4 的方阵。我们事先给每个生肖分配了一个 0000 到 1111 之间的编号(所以 16 个编号只用到 12 个)。分配的时候顺序故意是乱的,这样板子上的孔更没规律,魔术效果更好。板子 1A 上印着右起第 1 位是 0 的生肖,并且这些生肖对应的位
...继续阅读
(13)
发表于
2023-01-22 07:23:29
每个面都是凹多边形的多面体

发表于
2023-01-22 07:23:29
每个面都是凹多边形的多面体
昨晚做梦,梦见了一个有趣的数学问题:有没有什么多面体,它的每个面都是凹多边形?有趣的是,接下来我梦见自己醒了过来,然后立即上网寻找答案。我梦见我查到了相关的论文,论文作者的名字中出现了很多奇怪的符号。我梦见我开始研究论文作者的名字该怎么发音。我梦见我研究了半天没有进展,于是踏上了拜访作者本人的路……然后就彻底醒了。然后立即上网寻找答案。废话不多说了。Branko Grünbaum 和 G. C. Shephard 在 1998 年的论文《Isohedra with Nonconvex Faces》中给出了一些例子。下图是我很喜欢的一个例子。整个多面体由12个全等的凹多边形组成。
...继续阅读
(13)
发表于
2022-06-24 02:29:20
16 年后重谈 P 和 NP
2006 年,我在博客(当时还是 MSN Space)上发了《什么是 P 问题、NP 问题和 NPC 问题》一文。这是我高二搞信息学竞赛时随手写的一些东西,是我的博客中最早的文章之一。今天偶然发现,这篇现在看了恨不得重写一遍的“科普”竟仍然有比较大的阅读量。时间过得很快。《星际争霸》(StarCraft)出了续作,德国队 7 比 1 大胜东道主巴西,《学徒》(The Apprentice)里的那个家伙当了总统,非典之后竟然出了更大的疫情。现在已经是 2022 年了。这 16 年的时间里,我读了大学,出了书,娶了老婆,养了娃。如果现在的我写一篇同样话题的科普文章,我会写成什么样呢?正好,我的新书《神机妙算:一本关于算法的闲书》中有一些相关的内容。我从书里的不同章节中摘选了一些片段,整理加工了一下,弄出了下面这篇文章,或许能回答刚才的问题吧。有一天,我和老婆去超市大采购。和往常一样,结完账之后,我们需要小心谨慎地规划把东西放进购物袋的顺序,防止东西被压坏。这并不是一件容易的事情,尤其是考虑到各个物体自身的重量和它能承受的重量之间并无必然联系。鸡蛋、牛奶非常重,但同时也很怕压;毛巾、卫生纸都很轻,但却能承受很大的压力。于是,我突然想到了这么一个问题:给定 n 个物体各自的重量和它能承受的最大重量,判断出能否把它们叠成一摞,使得所有的物体都不会被压坏(一个物体不会被压坏的意思就是,它上面的
...继续阅读
(18)
发表于
2022-06-24 02:29:20
16 年后重谈 P 和 NP
2006 年,我在博客(当时还是 MSN Space)上发了《什么是 P 问题、NP 问题和 NPC 问题》一文。这是我高二搞信息学竞赛时随手写的一些东西,是我的博客中最早的文章之一。今天偶然发现,这篇现在看了恨不得重写一遍的“科普”竟仍然有比较大的阅读量。时间过得很快。《星际争霸》(StarCraft)出了续作,德国队 7 比 1 大胜东道主巴西,《学徒》(The Apprentice)里的那个家伙当了总统,非典之后竟然出了更大的疫情。现在已经是 2022 年了。这 16 年的时间里,我读了大学,出了书,娶了老婆,养了娃。如果现在的我写一篇同样话题的科普文章,我会写成什么样呢?正好,我的新书《神机妙算:一本关于算法的闲书》中有一些相关的内容。我从书里的不同章节中摘选了一些片段,整理加工了一下,弄出了下面这篇文章,或许能回答刚才的问题吧。有一天,我和老婆去超市大采购。和往常一样,结完账之后,我们需要小心谨慎地规划把东西放进购物袋的顺序,防止东西被压坏。这并不是一件容易的事情,尤其是考虑到各个物体自身的重量和它能承受的重量之间并无必然联系。鸡蛋、牛奶非常重,但同时也很怕压;毛巾、卫生纸都很轻,但却能承受很大的压力。于是,我突然想到了这么一个问题:给定 n 个物体各自的重量和它能承受的最大重量,判断出能否把它们叠成一摞,使得所有的物体都不会被压坏(一个物体不会被压坏的意思就是,它上面的
...继续阅读
(17)
发表于
2021-12-13 04:39:48
一些有趣的环面多面体
发表于
2021-12-13 04:39:48
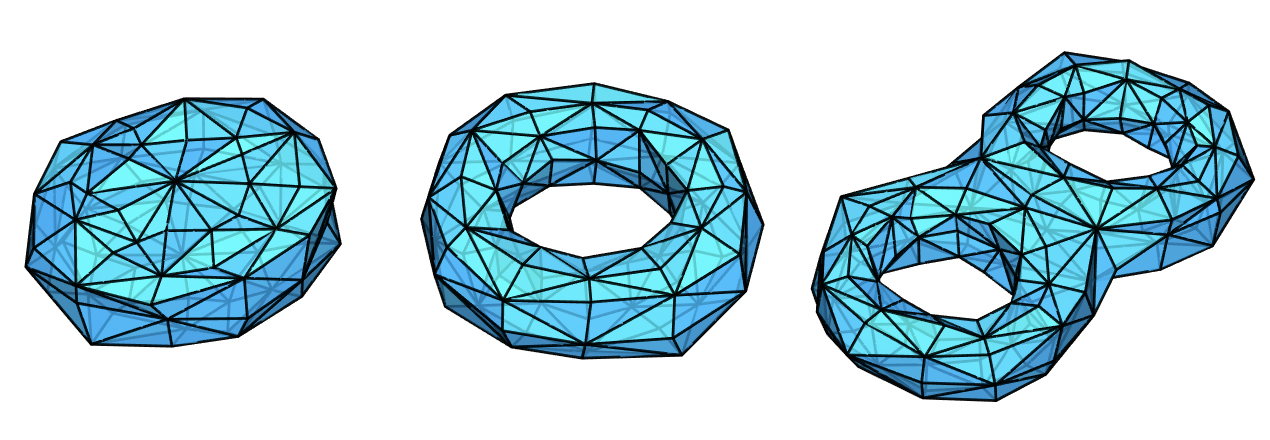
一些有趣的环面多面体

发表于
2021-09-12 12:18:56
趣题:切完大饼和蛋糕,让我们切一切甜甜圈
发表于
2021-09-12 12:18:56
趣题:切完大饼和蛋糕,让我们切一切甜甜圈
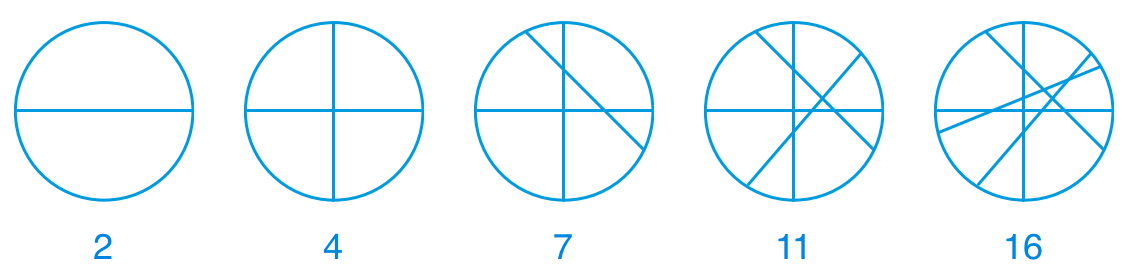
我正在餐桌前吃早餐。餐桌上有一张圆形的大饼,有一个方形的蛋糕,还有一个甜甜圈。我依次思考了下面三个问题。你能帮我想出它们的答案吗?3 刀切一张圆形的大饼,最多能把它分成多少块?或者说,3 条直线最多能把一个圆盘分成多少个区域?4 刀切一个方形的蛋糕,最多能把它分成多少块?或者说,4 个平面最多能把一个正方体分成多少个区域?3 刀切一个甜甜圈,最多能把它分成多少块?或者说,3 个平面最多能把一个(实心的)环面分成多少个区域?提示:上一个问题的答案总会为下一个问题提供线索。3 刀切一张圆形的大饼,最多能把它分成多少块?或者说,3 条直线最多能把一个圆形分成多少个区域?这是一个经典的小学问题。答案是 7 块。如图所示,事实上,当直线数分别为 1, 2, 3, 4, 5, …时,最多产生的区域数对应地是 2, 4, 7, 11, 16, …。这背后的规律是:1 条直线能把圆盘分成 2 个区域;第 2, 3, 4, 5, …条直线,则会让区域数增加 2, 3, 4, 5, …个。1 条直线最多能把圆盘分成 2 个区域,这事儿很显然。为什么第 n 条直线会让区域数增加 n 呢?这背后有一个非常简单的解释。前 n − 1 条直线会与第 n 条直线产生最多 n − 1 个交点,把第 n 条直线切成最多 n 段。仔细想想第 n 条直线上的每一段意味着什么——意味着某一个原有区域被细分成了两个新的区
...继续阅读
(11)
发表于
2021-09-06 16:25:16
称假币问题的变形:无假币与“天平机”
发表于
2021-09-06 16:25:16
称假币问题的变形:无假币与“天平机”
大家应该听说过 9 枚硬币的问题吧。9 枚硬币当中有 8 枚是真币,有 1 枚是假币。所有的真币重量都相同,假币的重量则稍重一些。怎样利用一架天平两次就找出哪一枚硬币是假币?方法是,先把 9 枚硬币分成三组,每组各 3 枚硬币。然后,把第一组放在天平左边,把第二组放在天平右边。如果天平向左倾斜,说明假币在第一组里;如果天平向右倾斜,说明假币在第二组里;如果天平平衡,说明假币在剩下的第三组里。现在,假币的嫌疑范围就被缩小到 3 枚硬币之中了。选择其中 2 枚硬币分放在天平左右两侧。类似地,如果天平左倾,就说明左边那枚硬币是假的;如果天平右倾,就说明右边那枚硬币是假的;如果天平平衡,就说明没放上去的那枚硬币是假的。9 硬币问题实在是太经典了,你甚至能在人教版小学五年级下册的课本里看到它。9 硬币问题还衍生出了很多变形,其中最著名的当属 12 硬币问题了:有 12 枚硬币,其中一枚是假币,但我们不知道假币是更重一些还是更轻一些;请利用一架天平三次找出哪一枚硬币是假币,并判断出它比真币更重还是更轻。12 硬币问题的经典程度恐怕不亚于 9 硬币问题。早在 20 世纪 40 年代,12 硬币问题就已经吸引了一大批数学家和数学爱好者,甚至有人建议把这个问题扔到德国去,以削弱德国人在二战中的战斗力。如果你想知道答案,可以在网上找找,应该很容易找到。我们今天就不讨论了。今天,我们真正想聊的其实是这个
...继续阅读
(14)
发表于
2021-09-05 16:03:12
UyHiP 趣题:能否把一个凸四边形分成若干个凹四边形
发表于
2021-09-05 16:03:12
UyHiP 趣题:能否把一个凸四边形分成若干个凹四边形
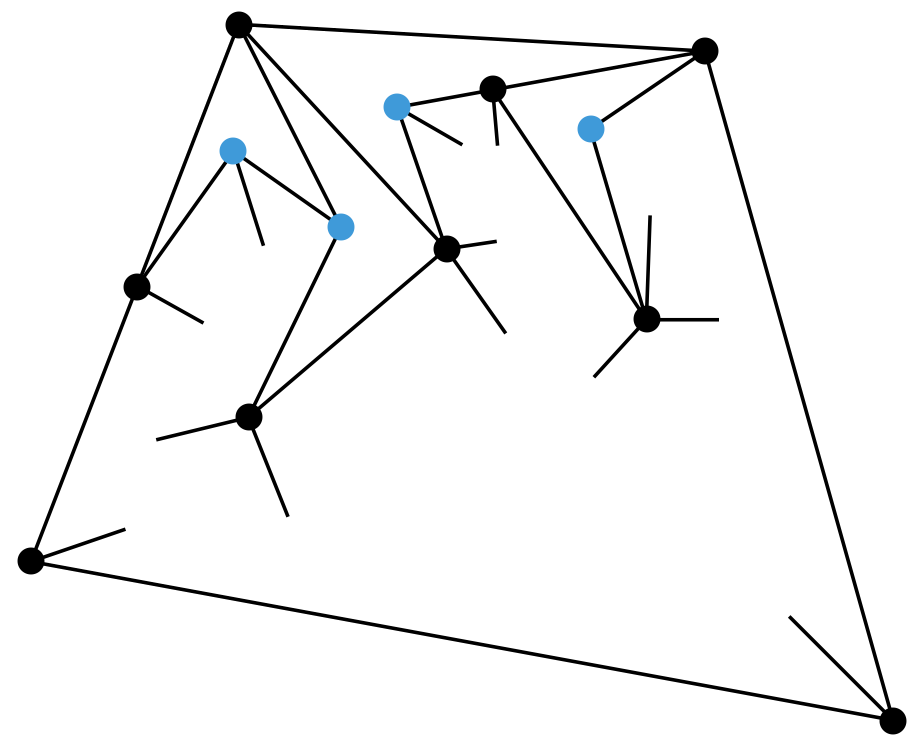
下面这个趣题出自Using your Head is Permitted 谜题站 2016 年 10 月的题目:能否把一个凸四边形分成若干个凹四边形?答案是否定的。我们给出一个非常漂亮的证明。在下面的文字中,我们用“优角”一词来表示一个大于 180 度小于 360 度的角。假设某个凸四边形被分成了若干个凹四边形。容易看出,每个凹四边形的内角中都有且仅有一个优角(如果没有优角,它就不是凹四边形;如果有两个或更多的优角,就与四边形内角和为 360 度矛盾)。现在,让我们把每个凹四边形的那个优角顶点涂成蓝色。容易看出,每个蓝色顶点只能成为一个凹四边形的一个优角顶点(否则汇聚于该点处的角度之和会超过 360 度)。这意味着,每个蓝色顶点都唯一地对应一个凹四边形。如果图中的蓝色顶点一共有 n 个,那么凹四边形也一共有 n 个。我们用两种不同的方式来统计所有凹四边形的所有内角的度数之和。汇集在每个蓝色顶点的内角之和都是 360° ,汇集在原四边形四个顶点处的内角之和也是一个 360° ,所以我们已经有至少 n × 360° + 360° 了。考虑到其他没涂成蓝色的顶点处还有很多角,因此上面这个数目实际上还会更多。但是,我们一共有 n 个凹四边形,每个凹四边形的内角之和是 360° ,因此所有凹四边形的所有内角之和显然应该是 n × 360° 。这个矛盾说明,我们无法把一个凸四边形分成若干个凹四
...继续阅读
(12)
发表于
2016-10-18 15:32:59
Lissajous 曲线的动画演示
发表于
2016-10-18 15:32:59
Lissajous 曲线的动画演示
随着常数 m 和 n 的变化,参数方程 x = sin(m · t), y = sin(n · t) 将会画出一系列漂亮的曲线。法国物理学家 Jules Antoine Lissajous 曾在 1857 年研究过这类曲线,因此人们把它叫做 Lissajous 曲线。我在reddit上看到了一个 Lissajous 曲线的动画演示,觉得看起来确实非常爽;但那个动画里没有解释曲线的生成方法,很多细节也有让人不太满意的地方,于是决定自己制作一个。这个动画展示的是 m = 13, n = 18 时的 Lissajous 曲线。
...继续阅读
(13)
发表于
2016-10-02 05:08:47
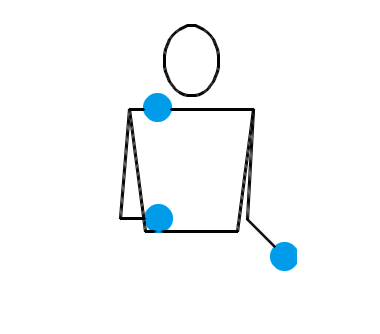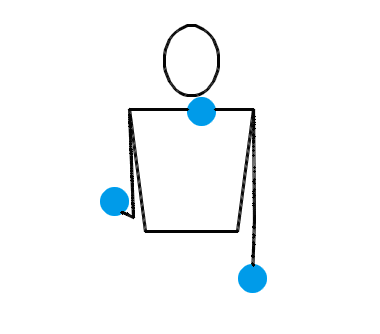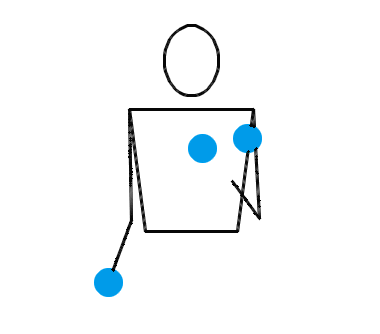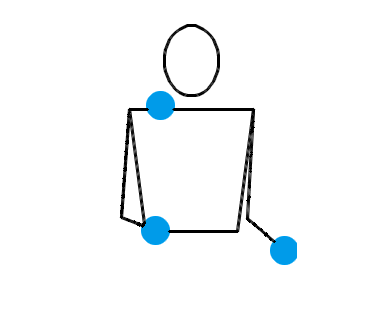
位换记号、排列测试与状态图:杂耍中的数学
发表于
2016-09-03 20:21:23
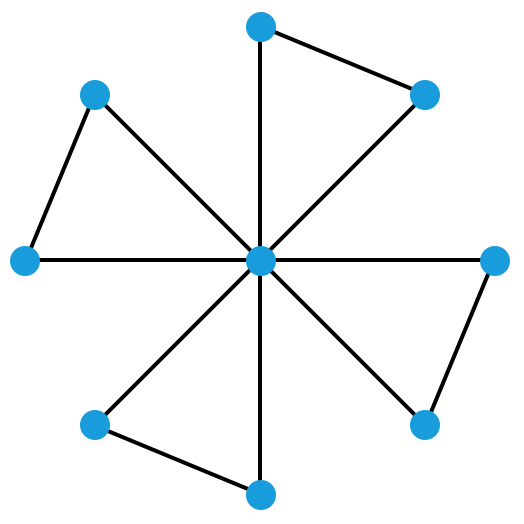
UyHiP 趣题:几个特殊的强正则图
发表于
2016-09-02 14:00:51
趣题:为什么偏偏是 6 格?
发表于
2016-08-24 01:22:05
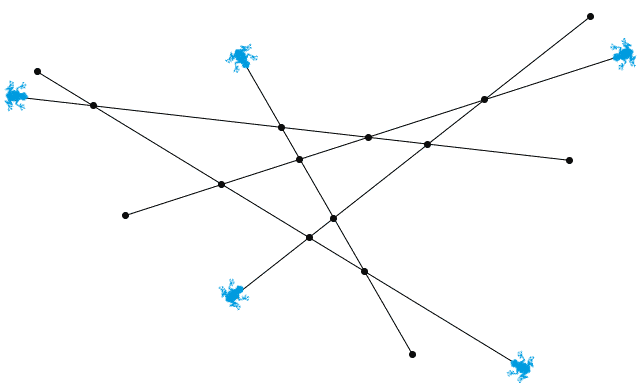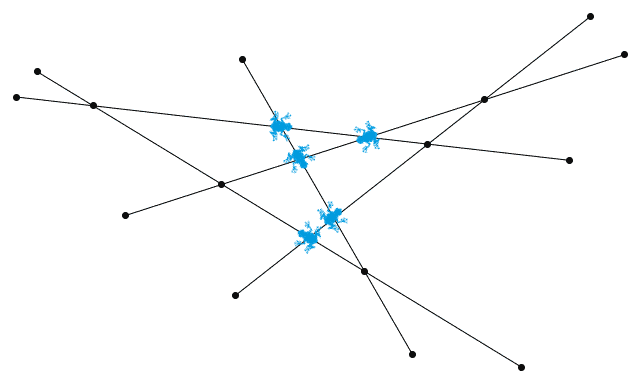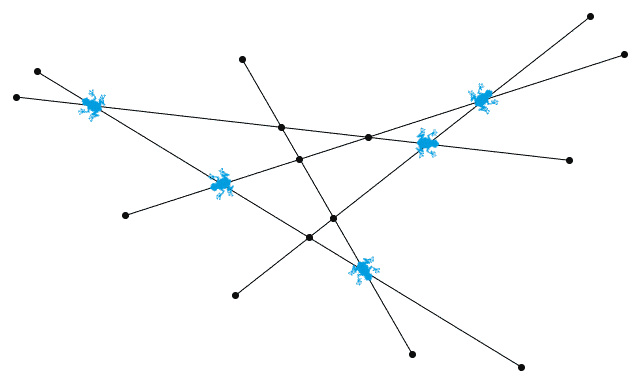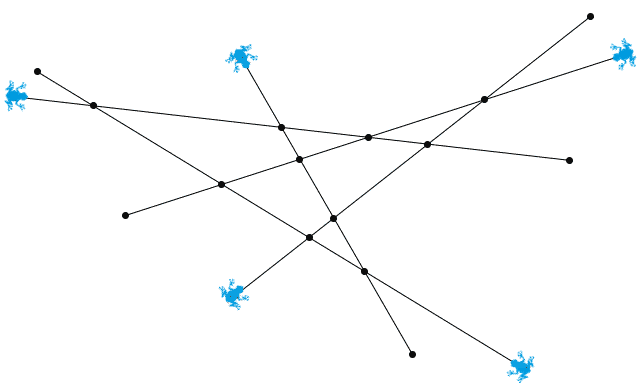
IMO2016 趣题:Geoff 的青蛙
发表于
2016-06-21 15:02:30
捡石子游戏、 Wythoff 数表和一切的 Fibonacci 数列
发表于
2016-05-02 14:52:06
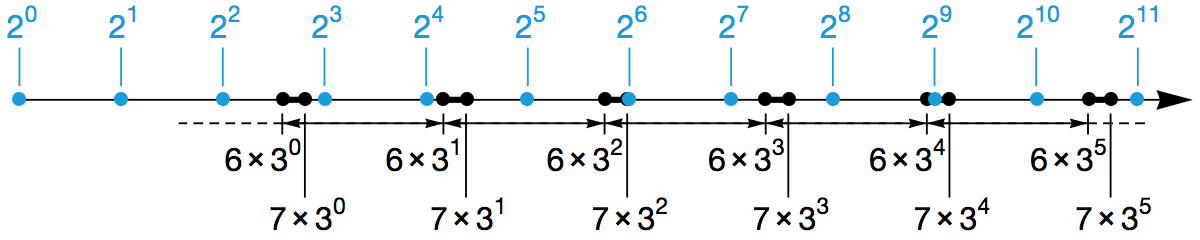
如果把 3 · n + 1 问题改为 3x · n + 1 问题
发表于
2016-04-30 03:38:17
趣题:两个方阵是怎样互相穿过对方的?