发表于
2025-06-29 11:38:22
最近

发表于
2025-06-20 07:32:37
云数据库行业动态@2025-06-20
标题:openGauss 发布 MCP Server支持SQL查询/运维管理等功能;阿里云PostgreSQL发布承诺型Serverless重要更新openGauss 发布 MCP Server[1],面相LLM提供更为便捷的SQL执行能力、此外还可以帮助开发者更为快捷的实现用户管理,安装,监控等能力(DataKit MCP Server)。更新详情RDS高可用系列和集群系列提升多可用区部署实例的SLA,双可用区统一提升至99.995%,三可用区及以上统一提升至99.997%。[4]RDS PostgreSQL发布承诺型Serverless能力,该能力是指在已购买的固定规格RDS PostgreSQL实例上(计费类型包括包年包月或按量付费)启用Serverless功能。[5]RDS PostgreSQL 17新增支持插件AI(rds_ai)(1.0.0)、高速全文检索(RUM)(1.3)、定时任务(pg_cron)(1.6)和pg_partman(5.2.4);RDS PostgreSQL 14~15版本新增支持插件AI(rds_ai),版本为1.0.0。RDS PostgreSQL 13新增支持插件SQL限流(rds_ccl),版本为1.2[6]RDS PostgreSQL支持全球多活数据库,该方案基于RDS PostgreSQL的原生物理复制与数据传输服务(DTS),实现了一站
...继续阅读
(11)
发表于
2025-06-06 02:36:22
云数据库行业动态@2025-06-06
标题:MariaDB收购高可用产品Galera;ClickHouse融资$3.5亿;Snowflake $2.5亿收购Crunchy Data重要更新在Databricks以10 亿美元收购Neon后,Snowflake以2.5亿美元收购Crunchy Data,一家深度PostgreSQL产品服务商。来自“fairchild”的评论:“它预示着AI Agent将成为数据库资源的主要消费者和创建者,这将从根本上改变数据库的交互模式——从人类驱动转变为机器驱动”。[2]MariaDB宣布收购高可用产品Galera Cluster。这两个产品一直以来合作紧密,MariaDB通过此次收购,可以向客户提供更具竞争力的企业级高可用方案;而对于Galera Cluster则可以获得更多可靠的客户。[1]ClickHouse宣布融资3.5亿美元C轮融资,本次融资将主要用于全球化业务推进、AI与分析能力增强等方向。其他建议关注的重要更新:Amazon Neptune 宣布推出 MCP(模型上下文协议)服务器[75]TDSQL-C MySQL 版发布全球数据库功能,帮助企业构建高可用、低延迟、强一致的全球数据库架构。[83]Aurora DSQL 现已全面GA[78]更新详情阿里云RDS MySQL标准版高可用云盘主实例新增128核512 GB规格(mysql.x4.16xlarge.2c)。[4]
...继续阅读
(25)
发表于
2025-05-25 09:13:59
使用Oracle云上的MySQL作为向量存储
MySQL的向量处理现状向量数据库或者说向量处理是,个人认为,最为重要数据库AI能力。目前,各个数据库都在围绕着向量数据库构建更为丰富的LLM/AI相关功能。而MySQL 9最为重要的特性之一就是新增了向量处理能力。当前的版本主要包括了:(a) 向量数据类型;(b) 简单的向量处理函数。其中部分向量处理函数放在了MySQL的企业版或云版本中。因为当前MySQL 9系列的版本均为创新版(并不是稳定版),所以相关功能还会不断的迭代和发展。期待未来做出更多丰富功能:(a) 新增向量相似性搜索功能;(b) 并将完整的向量处理能力放到社区版中。后续依旧会持续关注这部分的产品能力。本文测试环境为Oracle Cloud,你可以参考在 Oracle 云上免费测试数据库[3]文中创建一个免费的MySQL实例进行测试。MySQL中的向量数据类型向量数据存储在MySQL 9中新增了数据类型vector用来存储向量数据[1],简单的使用方式如下:create table vector_t01 (
id int,
s_v_01 vector(390),
s_v_02 vector(390)
);这里表示s_v_01、s_v_02均为390维的向量,每个维度在MySQL中使用4 bytes的单精度浮点类型存储。写入向量数据为了测试使用方便,这里使用string_to_vector对向
...继续阅读
(263)
发表于
2025-05-25 09:13:59
使用Oracle云上的MySQL 9.x作为向量存储
MySQL的向量处理现状向量数据库或者说向量处理是,个人认为,最为重要数据库AI能力。目前,各个数据库都在围绕着向量数据库构建更为丰富的LLM/AI相关功能。而MySQL 9最为重要的特性之一就是新增了向量处理能力。当前的版本主要包括了:(a) 向量数据类型;(b) 简单的向量处理函数。其中部分向量处理函数放在了MySQL的企业版或云版本中。因为当前MySQL 9系列的版本均为创新版(并不是稳定版),所以相关功能还会不断的迭代和发展。期待未来做出更多丰富功能:(a) 新增向量相似性搜索功能;(b) 并将完整的向量处理能力放到社区版中。后续依旧会持续关注这部分的产品能力。本文测试环境为Oracle Cloud,你可以参考在 Oracle 云上免费测试数据库[3]文中创建一个免费的MySQL实例进行测试。MySQL中的向量数据类型向量数据存储在MySQL 9中新增了数据类型vector用来存储向量数据[1],简单的使用方式如下:create table vector_t01 (
id int,
s_v_01 vector(390),
s_v_02 vector(390)
);这里表示s_v_01、s_v_02均为390维的向量,每个维度在MySQL中使用4 bytes的单精度浮点类型存储。写入向量数据为了测试使用方便,这里使用string_to_vector对向
...继续阅读
(150)
发表于
2025-05-23 00:33:00
云数据库行业动态@2025-05-23
标题:OceanBase发布PowerRAG 、共享存储和桌面版;AWS支持PostgreSQL 18;庆祝MySQL 30活动将与成都举行重要更新OceanBase发布PowerRAG、共享存储和桌面版[1]。其中PowerRAG功能是由OB Cloud上的OceanBase提供的全新功能,支持文档存储、分片到向量检索等功能[2];“共享存储”则可以更好的适配各类云存储架构;桌面版则可以在2c6g的环境完成OceanBase部署与体验。ACMUG(中国MySQL用户组)组织的庆祝MySQL 30周年,暨ACMUG年度分享,将于23~24日于成都举行,感兴趣的可以去现场与MySQLer们面基。时间:5月23日-24日(13:00-17:50);地址:成都市武侯区吉庆四路188号IMC国际广场成都书声科技(叫叫)四楼演播厅[3]。更新详情阿里云RDS MySQL全球多活数据库(GAD)支持更多海内外地域。[4]RDS MySQL标准版云盘只读实例新增128核512 GB规格。[5]RDS PostgreSQL的大版本升级功能在蓝绿部署和本地升级等模式的基础上,新增了零停机模式[6]RDS SQL Server新增监控指标sqlserver.alwayson_lagsecs[7]Azure(微软云)Cosmos DB支持使用 DiskANN 进行过滤向量搜索[10]Azure Back
...继续阅读
(27)
发表于
2025-05-18 01:48:08
MySQL JSON Path :使用与示例
随着 MySQL 对 JSON 类型的原生支持,操作 JSON 数据已变得非常高效与强大。在过去数年的版本中,MySQL 也在不断地增强 JSON 处理相关的功能。在 JSON 处理中需要非常频繁的使用“JSON Path” 语法,而这部分又是略微复杂的部分,本文将系统的介绍如何在 MySQL 中使用 JSON Path,包括语法规则、各种通配符用法、递归匹配等高级技巧,并通过丰富示例帮助开发者快速掌握。什么是 JSON Path?JSON Path是一种表示法,用来描述如何在 JSON 文档中定位数据。类似于文件系统路径,JSON Path 指引着从 JSON 根节点出发,逐步深入结构内部。在 MySQL 中,几乎所有的JSON相关的函数都会使用到,包括:JSON_EXTRACT()、JSON_SET()、JSON_REPLACE()、JSON_REMOVE()、JSON_CONTAINS()等。我们看到的场景的写法类似于:$.name、$.colors[0]、$.store**.price等。基础语法说明JSON Path的基础语法,遵循以下规则:$:表示 JSON 文档的根节点。.:用于访问对象中的属性。["key"]:另一种访问对象属性的方式,适合处理特殊字符的 key。[index]:访问数组中的元素。*:通配符,匹配所有子元素。**:递归通配符,匹配所有嵌套层级的元素[
...继续阅读
(35)
发表于
2025-05-16 00:44:00
云数据库行业动态@2025-05-16
标题: OceanBase创始人阳老师荣誉退休,致敬并祝福;Databricks10亿美金收购创新数据库Neon;MySQL 30周年中国区活动下周举行重点更新OceanBase创始人阳老师荣誉退休,致敬并祝福[11]。Redis从SSPL协议改成更被社区接受的AGPL协议, 并发布 8.0 版本[10]。Databricks持续并购,将以 10 亿美元收购极具创新架构的开源数据库 Neon[1][2]。Neon 提供了Serverless、扩展能力极强、具备非常好的AI特性的数据库服务,Neon 在架构上最大限度的利用了云基础设施能力,如对象存储的性能/持久性/扩展性/可复制性等、EC2的快速扩展/随时可用等,再叠加了PostgreSQL极强的生态能力。MySQL30周年中国区活动将于下周再成都举行,感兴趣的可以去现场围观[3]。时间:5月23日-24日(13:00-17:50);地址:成都市武侯区吉庆四路188号IMC国际广场成都书声科技(叫叫)四楼演播厅[3]。其他值得关注的产品更新包括:Google MCP 数据库工具箱支持 Bigtable 连接器[63]OCI上Oracle Database 23ai 支持使用数据库内转换模型与 Select AI RAG 结合使用,简化向量模型处理[84]更新详情阿里云RDS MySQL标准版云盘只读实例新增128核512 GB规格(
...继续阅读
(32)
发表于
2025-05-09 11:56:38
在 Oracle 云上免费测试数据库
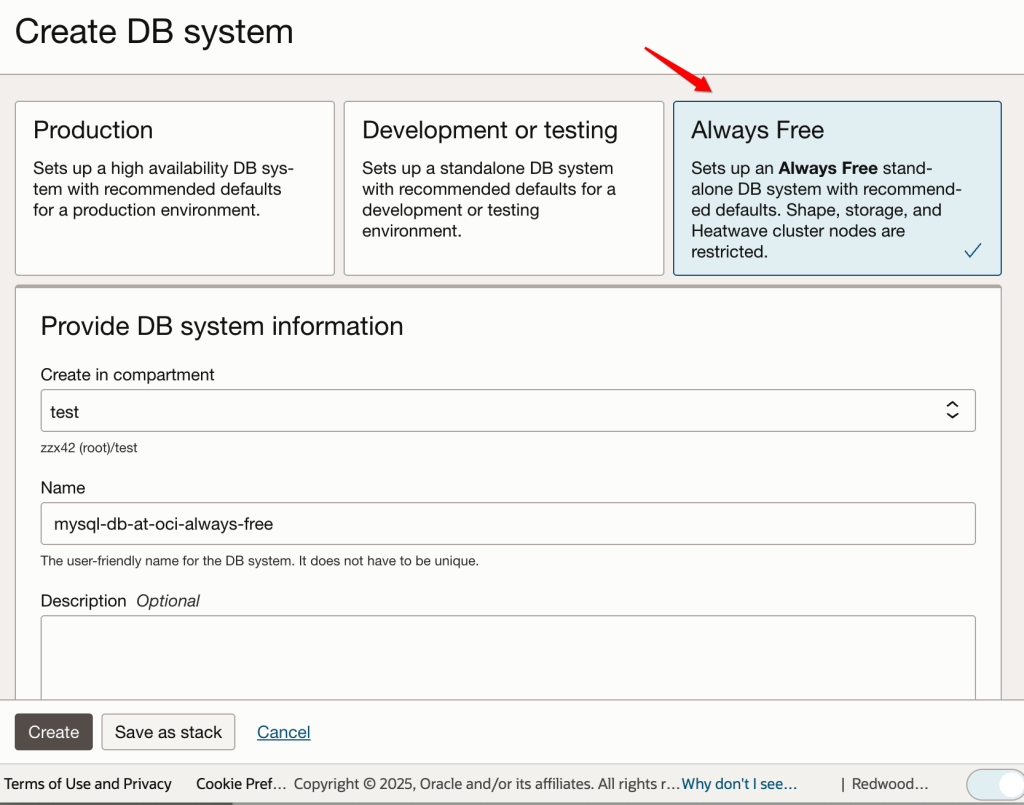
发表于
2025-05-05 14:44:38
Protected: 古城荆州
This content is password protected. To view it please enter your password below:Password:
...继续阅读
(31)
发表于
2025-05-05 03:17:29
理解 NumPy 中的高维数组
在机器学习中大量的使用NumPy作为其基础的数据结构,ndarray是NumPy的核心数据对象。对于ndarray高维数组的一个非常容易产生的误解是,使用数学中的矩阵(或者叫“行列式”)概念去尝试理解更高维的场景,或者使用更高维空间去理解,这样都会导致难以较好的理解更高维(5或6维)的数组。本文使用较为直观的示例和可视化的展示,更为“标准”(文档推荐的)的方式去理解ndarray的更高维数组。更多详细内容,可以参考阅读:numpy.ndarrayNumPy: the absolute basics for beginners问题在机器学习中,经常要对多维的数组做各种操作。对高维数组建立更好的直觉理解,则有利于去理解这些操作。例如,我们考虑右侧的代码,想一想该代码的输出是什么?>>> import numpy as np
>>> np.array([[[1],[2]],[[3],[4]]]).shape
(考虑输出是什么)要回答这个问题,则需要建立对于多维数组结构的理解。文档中对于高维数组理解的建议在NumPy: the absolute basics for beginners中有如下一段话:It is familiar practice in mathematics to refer to elements of a matrix by the row index first a
...继续阅读
(35)
发表于
2025-05-01 09:14:34
Oracle LogMiner 使用
在Oracle官方文档Using LogMiner to Analyze Redo Log Files[2]中,对该功能有详细的介绍,包括了LogMiner的配置与使用、数据过滤、补充日志(Supplemental Logging)、使用示例等。Oracle 何时引入的LogMiner?自 1999 年发布 Oracle 8i 的时候,正式引入 LogMiner 功能(参考:Redo Log Analysis Using LogMiner[1])。该功能支持以SQL的形式分析redo中的数据,最初考虑的应用场景,主要还是偏于故障恢复、异常诊断、审计等,但是该功能的潜力很大,现在已经逐步成为Oracle CDC的主流方案之一。目前已经有很多的集成/同步工具都使用LogMiner进行变化数据获取,虽然,目前官方依旧不推荐这么做,文档中的原文如下:“Note:LogMiner is intended for use as a debugging tool, to extract information from the redo logs to solve problems. It is not intended to be used for any third party replication of data in a production environment.”根据经验来看,L
...继续阅读
(32)
发表于
2025-04-26 10:31:26
MySQL/InnoDB 锁诊断:间隙锁
为什么需要间隙锁关于为什么需要 “Gap Locks” 或者 “Next-key Locks” ,在MySQL的文档“17.7.1 InnoDB Locking”的小节中有较为详细的介绍,这里不再赘述。这里使用一个具体的示例,以便开发者方便构造与观察间隙锁。在Repeatable-Read隔离级别下,在整个事务的过程中,数据需要保持一致,经常需要使用间隙锁对数据或资源进行保护。例如,在如下的事务中:DROP TABLE IF EXISTS t1;
CREATE TABLE t1 (
id int,
nick varchar(32),
age int,
KEY ind_n (nick),
PRIMARY KEY (id)
);
INSERT INTO t1 VALUES ( 1, "a", 27 );
INSERT INTO t1 VALUES ( 11, "k" ,23 );
INSERT INTO t1 VALUES ( 24, "x" ,22 );
START TRANSACTION;
SELECT * FROM t1 WHERE nick >= "k" for update;
+----+------+------+
| id | nick | age |
+----+------+------+
| 11 | k | 23 |
| 24
...继续阅读
(35)
发表于
2025-04-25 02:57:00
云数据库行业动态@2025-04-25
标题:阿里云开源RDS MCP Server发布;火山云MySQL发布Sequence、Flashback Query等功能重要更新阿里云数据库发布开源RDS MCP Server,支持快速实例创建、实例状态诊断等功能:现已开源|阿里云RDS发布MCP Server能力,解锁数据库“对话即运维”新体验。火山云数据库 MySQL 发布一系列重磅功能,包括了Sequence Engine[5]、Flashback Query[6]、5.7到8.0大版本升级等[7]。更新详情火山云(字节)云数据库 MySQL 支持对表/列级别进行账号权限控制[4]云数据库 MySQL 8.0 版本实例提供了 Sequence Engine,用于获取唯一递增序列值[5]云数据库 MySQL 8.0 实例中提供闪回查询(Flashback Query)功能[6]支持了云数据库 MySQL 5.7 到 8.0 的升级功能[7]云数据库 PostgreSQL 开始支持支持 17[26]云数据库 PostgreSQL提供 1.5.2 版本的 pg_repack 插件[27]在 PostgreSQL 13 及以上版本实例中提供 0.8.0 版本 pg_vector 插件[28]云数据库 PostgreSQL 支持插件 pg_partman、pg_jobmon[30]缓存数据库 Redis 版支持了跨地域备份恢复到
...继续阅读
(30)
发表于
2025-04-20 07:03:33
使用 Docker 工具安装不同版本的Oracle数据库

发表于
2025-04-18 10:42:47
云数据库行业动态@2025-04-18
标题:Google AlloyDB自持内置自然语言查询功能;达梦2024年营收为10.4亿,同比增长31%重要更新达梦发布2024年度报告,该年年度营收达10.4亿,同比增长31.49%,净利润为3.6亿。[1]Google AlloyDB 发布自然语言查询功能,该功能可以让开发者通过简单的配置,就可以在数据库内部实现自然语言转SQL并进行查询。[2]更新详情阿里云RDS MySQL全面提升本地盘实例(含主实例和只读实例)的存储空间上限,最高支持16000 GB,满足用户存储扩容需求。[4]RDS MySQL的秒级加列(Instant Add Column)通过变更数据字典的元数据来优化ADD COLUMN 操作。该功能避免了传统DDL操作对全表数据的修改或重建,实现加列操作在秒级内完成,且不受表数据量影响。[5]RDS PostgreSQL ESSD云盘实例支持下载带表头信息的CSV格式备份文件,可用于数据分析或离线归档等需求。[6]火山云(字节)veDB MySQL 支持闪回查询,通过闪回查询功能,能够直接查询过去某段时间时间内的历史数据。[7]veDB MySQL 支持 RETURNING 语法,支持在执行 INSERT、REPLACE、UPDATE、DELETE 等 DML 语句时,直接返回受影响的行数据[8]AWS(亚马逊云)Bedrock 知识库现在支持 Aurora
...继续阅读
(30)
发表于
2025-04-13 01:45:00
MySQL/InnoDB 的 隐式锁
InnoDB 的锁容易被忽略的细节是关于“隐式锁”(即:implicit locks)的存在。表现上,有的锁是存在的,但在使用SHOW ENGINE INNODB STATUS或者performance_schema.data_locks中却查看不到。最为常见的隐式锁是在写入(INSERT)时,当前事务会持有该记录对应的锁,但是在系统中,通常是查看不到的。但,如果发生了该锁冲突(或竞争)时,系统中则可以看到此类锁信息。本文重现了较为常见的隐式锁场景,包括:数据写入(INSERT)时的隐式锁、根据主键操作是可能产生的二级索引隐式锁等。帮助开发者能够更系统的理解,InnoDB 的锁机制。写入数据产生的隐式锁准备数据DROP TABLE IF exists t1;
CREATE TABLE `t1` (
`id` int unsigned,
`nick` varchar(32),
`age` int,
UNIQUE KEY `uk_n` (`nick`)
);mysql> desc t1;
+-------+--------------+------+-----+---------+
| Field | Type | Null | Key | Default |
+-------+--------------+------+-----+--------
...继续阅读
(33)
发表于
2025-04-11 01:23:53
云数据库行业动态@2025-04-11
标题:DBaaS服务商Tessell获 $6000万融资; OceanBase开发者大会几乎5月于广州举行重要更新多云数据库平台服务商Tessell获 $6000万 容灾。此次融资将用于进一步扩大市场覆盖,并计划推出基于 AI 驱动的对话式数据库管理服务[1]。2025 OceanBase开发者大会将于5月17日广州举行。本届大会以「当 SQL 遇见 AI」为主题,会上,OceanBase 还将重磅发布面向 AI 时代的一体化产品矩阵,并分享 TP、AP、KV 及 AI 能力的最新实践成果。[2]更新详情阿里云PolarDB 库表恢复功能支持恢复速度配置,根据所占用的IOPS越多,实际恢复速度越快。[5]PolarDB 账号管理新增全局只读账号[6]Azure(微软云)适用于基于 vCore 的 Azure Cosmos DB for MongoDB 的 Power BI 连接器发布(预览版)[8]“I/O 性能分析”支持了Azure 虚拟机上的 SQL Server[11]GCP(谷歌云)BigQuery 数据准备功能现已正式发布 (GA),它提供 Gemini 提供的 AI 驱动的数据清理、转换和数据扩充建议。支持使用 Dataform 进行可视化数据准备流程和流程调度。[14]Cloud SQL 现已支持Enterprise Plus 推荐器。根据您的应用程序工作负载和资源利
...继续阅读
(32)
发表于
2025-04-06 02:18:55
InnoDB 整数类型存储的sign bit的设置
存储引擎在存储整数时,一般会使用最高位作为标志位,标记存储的整数是正数还是负数(参考),最高位也被称为“most significant bit (MSb)”。通常,最高位为1则表示正数,最高位为0,则表示负数。更进一步的,负数则会通过补码(参考:two’s complement)的方式表示。但是,InnoDB没有使用这种方法。InnoDB 的整数存储在死锁诊断时,偶然注意到,InnoDB 在存储整数时,与一般的系统是不同的。例如,int 类型存储 1 的时候,使用的表示是:0x80000001。更多的示例可以参考右图:整数值InnoDB 表示10x80000001-10x7fffffff70x80000007-70x7ffffff9可以看到,这与一般的有符号型的整数存储是相反的。即:正数表示时,最高位(MSb)为1负数表示时,最高位(MSb)为0关于这个问题,在Stackoverflow上也有看到有部分用户有类似的疑问:mysql highest bit Whether is 1 or 0 , when column is designed signed inthow mysql represent two’s complement本文将讨论为什么会这样。考虑 8-bit 场景下的这里来回顾一下“体系结构”中的最为基础的一些知识吧。整数值绝对值绝对值的二进
...继续阅读
(39)
发表于
2025-01-17 02:32:47
云数据库行业动态@2025-01-17
标题:阿里云RDS发布AI插件,支持千问/文本向量等功能;腾讯云TDSQL全年零失误支持超60银行重要更新Gartner 数据库魔力象限完整报告正式对外发布,阿里云连续5年入选「领导者」象限,华为云进入挑战者象限[1][2]。阿里云 RDS PostgreSQL 现推出AI插件“rds_ai”,集成了阿里云百炼的先进模型,包括通义千问、通用文本向量和通用文本排序等。通过该插件,您可以在RDS PostgreSQL数据库中轻松实现包括大模型问答、文本向量转换、文本排序、Top N相似向量检索以及RAG问答等多种应用场景。此外,rds_ai还支持自定义模型,您可以灵活添加所需模型,以在RDS PostgreSQL中实现丰富多样的AI应用[3]。腾讯云数据库TDSQL支撑60+银行年终决算“零失误”。腾讯云数据库TDSQL和腾讯专有云TCE、专有云PaaS平台TCS、大数据平台TBDS、操作系统TencentOS、腾讯云TI平台等“6T“融合创新基础软件,为60多家银行及大型央企财务公司保驾护航,助力它们高效完成决算任务,并且「零失误」。[4]更新详情腾讯云云数据库 MySQL 8.0内核版本更新20240930。[27]TDSQL-C LinkTDSQL-C 支持将“只读分析引擎”加入到新数据库代理中[28]TDSQL-C 支持通过控制台查看“只读分析引擎”的监控信息、参数等信息。[2
...继续阅读
(40)
发表于
2025-01-12 03:46:59
Protected: 自动化测试云数据库 RDS MySQL 的性能
This content is password protected. To view it please enter your password below:Password:
...继续阅读
(35)
发表于
2025-01-10 02:59:24
云数据库行业动态@2024-01-10
标题:达梦冯裕才教授获CCF 2024最高科学技术奖;OceanBase 社区年终嘉年华将于周六在北京举行重要更新达梦数据库创始人冯裕才教授获2024年“CCF最高科学技术奖”[1]。获奖理由:“冯裕才教授是我国著名数据库科技工作者,长期致力于我国自主数据库的研发和产业化工作,突破了数据库共享存储集群技术,开发了达梦系列数据库,打造了国内首家数据库上市企业“达梦数据”,为推动我国基础软件产业的发展做出了重要贡献。”OceanBase 社区年终嘉年华将于周六在北京举行[2]。OceanBase 将携手 360、TuGraph,邀请 360、作业帮、Boss 直聘、好未来等企业的技术大咖,共话 OceanBase 在各行业的应用实践和技术选型心得。感谢可以现场参加。更新详情阿里云RDS PostgreSQL主实例高可用系列标准版独享规格上线大规格实例。[3]RDS SQL Server支持在RDS控制台手动删除具有SA权限的数据库账号。[4]火山云(字节)云数据库 MySQL支持手动对实例的内核小版本进行升级[5]云数据库 MySQL支持为实例创建跨地域的灾备实例(邀测),为实例提供跨地域的灾备能力[6]支持在特定时间段内发起实例变配、重启、迁移、升级版本等操作,以增强实例管理的灵活性[7]GCP(谷歌云)BigQuery 发布新版本的 JDBC 驱动程序][8]参考链接[1]http
...继续阅读
(30)
发表于
2025-01-04 03:12:28
使用MySQL实现车票秒杀的进阶挑战
这是第二次 SQL 编程大赛[1],我依旧是评委之一,所以自己也尝试了独立完成该问题的挑战。这次大赛分为“普通挑战”和“进阶挑战”。其中普通挑战较为简单,本文主要讨论自己完成进阶挑战过程中的想法与思路。问题描述原始的问题,可以参考:NineData 第二届数据库编程大赛 用一条SQL秒杀火车票,本文仅考虑其中的“进阶挑战”。这里该“进阶挑战问题”复述如下。有如下两张表存放着乘客信息和列车信息,使用一条SQL给每个乘客分配一趟列车以及对应的座位号,需要注意,需要考虑进阶挑战的一些要求,比如,每趟列车可以发售10%的无座车票;车票需要有限发售有座车票,然后才开始发售无座车票。mysql> desc passenger;
+-------------------+-------------+------+-----+
| Field | Type | Null | Key |
+-------------------+-------------+------+-----+
| passenger_id | varchar(16) | NO | PRI |
| departure_station | varchar(32) | NO | |
| arrival_station | varchar(32) | NO |
...继续阅读
(41)
发表于
2025-01-03 00:43:36
云数据库行业动态@2025-01-03
标题:各类数据库年终总结集中发布;PostgreSQL生态大会于本周六举行;华为云GaussDB/OceanBase不同报告各获第一重要更新第七届中国PostgreSQL数据库生态大会于本周六在上海举行,大会邀请了 PostgreSQL 社区相关开发、意见领袖、企业领军人物、资深用户与广大DBA、开发者参加。感兴趣的可以在上海现场参加[13]。华为云GaussDB,中国金融级分布式数据库市场No.1:根据沙利文联合头豹研究院发布《2024年金融级分布式数据库市场跟踪报告》,华为云GaussDB在2023年、2024年上半年中国金融级分布式数据库市场份额整体规模第一本地部署整体第一[14]OceanBase 获评分布式数据库市场份额第一:根据工信部赛迪顾问发布 2024 年《中国金融行业数据库市场研究报告》,OceanBase 获评分布式数据库市场份额第一!在银行、保险、证券三大子市场中,OceanBase 同样以综合评分第一的成绩位居榜首[15]本周是各类总结发布的一周,这里汇总部分供参考:2024 云数据库年度总结[1]Databases in 2024: A Year in Review[2]2024年度盘点|阿里云瑶池数据库的高光时刻[3]请回答2024|华为云数据库年度盘点[4]2024 OceanBase 年度报告 | 每一笔记录都算数[6]大事记 | 2024:进而有为
...继续阅读
(38)
发表于
2024-12-30 00:09:05
2024 数据库年度总结

发表于
2024-12-27 10:57:09
MySQL 8.0 中的 CTE 功能
CTE 的全称是 Common Table Expressions,有时候也缩写为 CTEs,在 SQL 标准中使用WITH clause表达[1]。在 ANSI standard 标准的 SQL:1999 中定义,参考:ISO/IEC 9075-2:1999[7][8]。该特性支持在 MySQL 8.0 中正式被引入[9]。通常,如果不需要编写特别复杂的 SQL ,更为具体的,如果无需编写带有递归功能的 SQL 时,CTE 通常都不是必须的。所以,该语法功能,对于分析型的场景或者数据开发等场景更为常用。这里概述 CTE 的两个常用功能:简化子查询结构、实现递归执行。其中,实现递归执行,是 CTE 独特的能力,是对 SQL 能力的一种补充。简化子查询结构CTE 功能提供了一种新的子查询或临时表的写法。可以把后续 SQL 中需要使用的临时表或子查询独立的放在WITH子句中,使得结构看起来更为清晰一些。例如,如下两个写法在语义上是等价的:WITH
t_mid as (
SELECT * FROM t_1 JOIN t_2
)
SELECT * FROM t_mid;SELECT *
FROM
(
SELECT * FROM t_1 JOIN t_2
) t_mid;递归执行该功能是 CTE 的核心能力。例如,在表中查询好友的好友、查询主管的主管、递
...继续阅读
(42)
发表于
2024-12-27 00:19:50
云数据库行业动态@2024-12-27
标题:Gartner 数据库魔力象限发布:华为云、SingleStore进入;Yugabyte推出;Amazon RDS 支持 MySQL 9.1重要更新Gartner 正式对外发布了 2024 年的数据库魔力象限[1]:依旧由Google、AWS、Azure、Oracle领跑;MongoDB、DataBricks、Snowflake则又向左上角前进了一些;阿里云则依旧保持在领导者象限。华为云则在时隔两年后,再次进入该象限。分布式数据库厂商 SingleStore 进入,而 Yugabyte 跌出。更新详情GCP(谷歌云)BigQuery 新增墨西哥地区支持[7]Cloud SQL Enterprise Plus 开始支持启用查询洞察[8]AlloyDB 支持通过 Cloud Monitoring 信息中心监控以下众多指标[13]火山云(字节)云数据库 veDB MySQL 版新增亚太东南 (柔佛) 地域售卖[17]AWS(亚马逊云)Amazon RDS 支持 MariaDB 11.4.4、10.11.10、10.6.20 和 10.5.27等小版本[18]Amazon RDS for Db2 支持多数据库能力[19]Amazon RDS 在数据库预览环境中支持 MySQL 9.1[20]Amazon RDS Proxy 新增 Aurora 和 RDS 上的 MySQL cachi
...继续阅读
(43)
发表于
2024-12-24 14:47:35
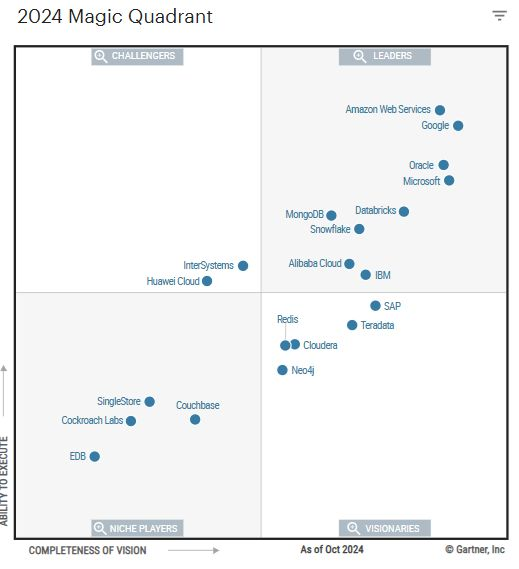
2024 Gartner 数据库魔力象限概要解读
发表于
2024-12-23 03:53:49
云数据库行业动态@2024-12-20
标题:GaussDB MySQL更为TaurusDB,全新发布HTAP功能;SQL编程大赛决赛答辩周五晚举行;重要更新华为云 TaurusDB 新增HTAP实时分析(标准版)功能,能同时服务OLTP和OLAP的混合混合负载场景。其中AP部分采用列式存储引擎,利用SIMD计算技术提升实时分析性能[31]。TaurusDB 即为原 GaussDB(for MySQL) ,于11月更名 TaurusDB[32]。12 月 14 日,Doris Summit Asia 2024 在深圳举办,该活动由飞轮科技主办,腾讯云和阿里云联合主办[1]。在12月07日,由 StarRocks 举办的 StarRocks Summit 在北京举办[2]。更新详情阿里云RDS MySQL基础系列常规实例支持免费的云盘加密功能,该功能将对整个数据盘上的数据进行基于块存储的加密,能够有效保障您的数据安全[4]RDS SQL Server Web版独享入门规格实例支持大版本升级[5]Azure(微软云)Azure Functions 支持 Azure Database for MySQL 绑定[6]GCP(谷歌云)Bigtable、 Memorystore for Redis 接入 Database Center 的支持,可让您集中查看整个数据库群 [8][9]数据库迁移服务现在支持 MySQL 次要版本 8.
...继续阅读
(52)
发表于
2024-12-22 02:24:49
使用PolarDB的并行查询优化大赛SQL
