发表于
2017-04-11 06:00:20
一文读懂机器学习、数据科学、深度学习和统计学之间的区别

发表于
2017-04-11 04:00:25
干货|关于数据科学的十本好书

发表于
2017-04-11 02:30:33
三问英特尔中国研究院院长宋继强:英特尔如何打通AI链条?

发表于
2017-04-10 23:00:57
聊天机器人之热(中篇):大玩家、创业者和投资人

发表于
2017-04-10 09:00:33
Facebook的数据预测工具Prophet有何优势?用贝叶斯推理一探究竟

发表于
2017-04-10 07:30:07
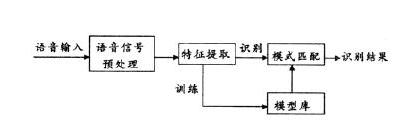
玩人工智能的你必须知道的语音识别技术原理
发表于
2017-04-10 06:00:36
语音识别取代搜索框:苹果Siri成为第二大搜索引擎
发表于
2017-04-10 04:30:54
深度学习也有缺陷,同质化的AI创业竞争将很残酷

发表于
2017-04-10 02:30:06
独家 | 对话斯坦福教授邢磊:AI医疗研究如何突破瓶颈?

发表于
2017-04-10 01:19:13
聊天机器人之热(上篇):微软、Facebook、亚马逊等巨头为何押下重注

发表于
2017-04-09 02:36:28
优秀人工智能电影,哪些你不可错过?

发表于
2017-04-08 23:00:23
机器学习从用户社交媒体资料中窥得的五种秘密

发表于
2017-04-07 23:00:18
为什么机器学习行业的发展离不开 “开源”

发表于
2017-04-07 09:00:11
7个小故事告诉你 当人工智能遇上医生会发生什么

发表于
2017-04-07 07:30:13
机器人客服真假难辨?!

发表于
2017-04-07 06:00:28
普通程序员如何转向AI方向

发表于
2017-04-07 04:30:25
摆好正确姿势 看 Google 神级深度学习框架 TensorFlow 的实践思路
发表于
2017-04-07 02:30:26
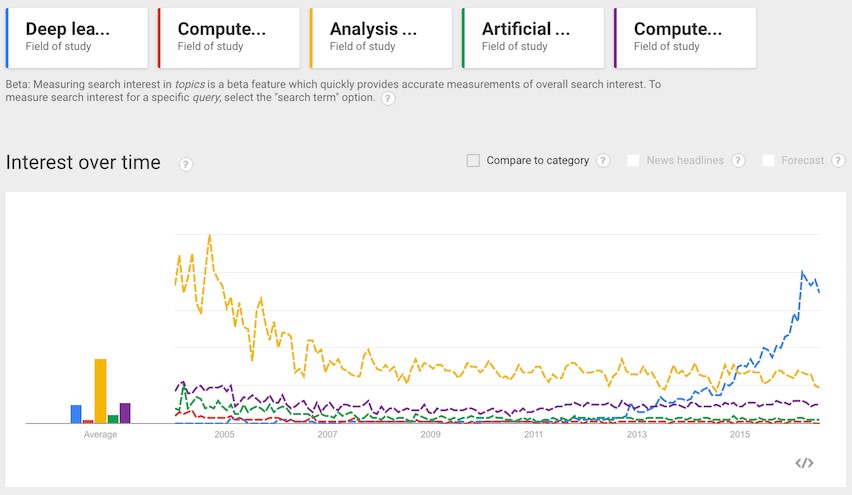
麦肯锡中国人工智能报告 直面三座大山

发表于
2017-04-06 23:00:59
语音合成到了跳变点?深度神经网络变革TTS最新研究汇总

发表于
2017-04-06 09:00:00
独家对话百度NLP:先解决语义理解,再谈机器翻译取代人类

发表于
2017-04-06 07:30:43
演讲 | 华院首席科学家:中文或是人类面对人工智能的最后壁垒

发表于
2017-04-06 06:00:32
深度学习真的万能吗?理解深度学习的局限性

发表于
2017-04-06 04:30:14
谷歌开源 Python Fire;一张图读懂 Python、R 的大数据应用等

发表于
2017-04-06 02:30:17
图灵奖获得者Berners-Lee,如今最关心哪些议题?

发表于
2017-04-05 23:00:38
【深度】详解梯度下降法的三种形式BGD,SGD以及MBGD
详解梯度下降法的三种形式BGD,SGD以及MBGD本篇文章目录如下:批量梯度下降法BGD原理讲解随机梯度下降法SGD原理讲解小批量梯度详解MBGD原理讲解具体实例以及三种实现方式代码详解三种梯度下降法的总结在应用机器学习算法时,我们通常采用梯度下降法来对采用的算法进行训练。其实,常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点。下面我们以线性回归算法来对三种梯度下降法进行比较。一般线性回归函数的假设函数为:对应的损失函数为:(这里的1/2是为了后面求导计算方便)下图作为一个二维参数(theta0,theta1)组对应能量函数的可视化图:下面我们来分别讲解三种梯度下降法批量梯度下降法BGD我们的目的是要误差函数尽可能的小,即求解weights使误差函数尽可能小。首先,我们随机初始化weigths,然后不断反复的更新weights使得误差函数减小,直到满足要求时停止。这里更新算法我们选择梯度下降算法,利用初始化的weights并且反复更新weights:这里代表学习率,表示每次向着J最陡峭的方向迈步的大小。为了更新weights,我们需要求出函数J的偏导数。首先当我们只有一个数据点(x,y)的时候,J的偏导数是:则对所有数据点,上述损失函数的偏导(累和)为:再最小化损失函数的过程中,需要不断反复的更新weights使得误差函数减小,更新过程如下:那么好了,每次参数
...继续阅读
(15)
发表于
2017-04-05 06:59:30
没有功能需求设计文档?对不起,拒绝开发!

发表于
2017-04-03 23:00:47
新浪付稳:揭秘微博如何10分钟快速应对百亿级访问量

发表于
2017-04-02 23:00:07
数据API经济与大规模数据流通:从水的寓言说起

发表于
2017-04-01 23:00:12
Facebook 为什么不涉足公有云市场?错过时机还是能力不够?

发表于
2017-04-01 08:31:46
BBC:大数据带来的弊病?近因效应
